WisFaq!

Raakkruis en raakvlak

Beste

Ik ben (zelfstandig) aan het leren over afgeleiden van meerdere veranderlijken. Ik heb vernomen dat je met de partiële afgeleiden een raakkruis/raakvlak kunt bekomen?

Mijn vraag aan u: Wanneer bekom je deze? M.a.w. wanneer heb je een raakvlak en wanneer een raakkruis? En is het bekom je de formule voor beiden op dezelfde manier?

Hartelijk dank

Roland
6-6-2017

Antwoord

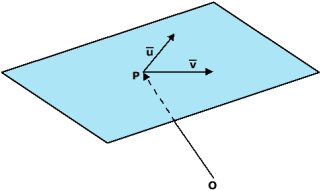
In de ruimte kan je vlakken weergeven als vectorvoorstelling. Het vlak door P kan je met twee richtingsvectoren schrijven als: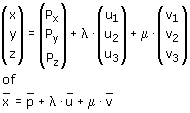



Als z=f(x,y) een raakvlak heeft in het punt P(a,b,f(a,b)) dan kan je een vectorvoorstelling van dat raakvlak zo vinden:



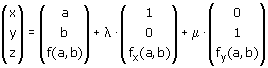
Je kunt deze vectorvoorstelling herleiden tot de volgende vergelijking:

z(x,y) = f(a,b) + f_x(a,b)(x-a) + f_y(a,b)(y-b)

Je hebt een `raakkruis' als de beide partiele afgeleiden bestaan; je hebt een raakvlak als de functie differentieerbaar is in dat punt.

• Partiële afleidbaarheid

WvR
6-6-2017