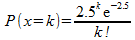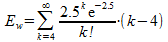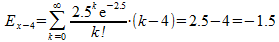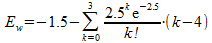WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Aantal te verwachten schepen

Het aantal schepen k per dag dat in een haven binnenkomt is poissonverdeeld met gemiddelde 2,5. De haven kan max 4 schepen per dag binnen laten. Wat is het verwachte aantal schepen dat per dag niet kan worden binnengelaten?

Ik weet $\lambda$=2,5 en ik ben P( X$\ge$ 5 ) = 1 - P (X$\le$ 4)= 0,1088 gaan berekenen.

Maar wat is nu mijn antwoord over het aantal schepen? Ik heb 0,1088·2,5=0,272 gedaan maar dit kan toch niet?

Dina
3de graad ASO - maandag 19 mei 2014

Antwoord

Hallo Dina,

Om een verwachtingswaarde te bepalen, moet je voor alle mogelijke uitkomsten uitrekenen:

kans x uitkomst

en deze waarden optellen.

In dit geval geldt:
Als x=aantal schepen dat aankomt, dan is de kans dat x=k:

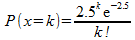
Het aantal schepen dat moet wachten, noem ik w. Voor dit aantal geldt:

w=k-4 (voor k$\ge$4)

Ik moet dus berekenen:

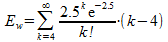
Dit is wel een lastige som, maar via een omweggetje kunnen we deze wel berekenen:
De verwachtingswaarde van het aantal schepen is 2,5. Als we even net doen alsof ook een negatief aantal schepen zou kunnen wachten (wanneer minder dan 3 schepen aankomen), dan zou de verwachtingswaarde van het aantal schepen dat moet wachten gelijk aan 4-2,5=-1,5.

We weten dus:

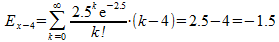
De termen met k=0 t/m k=3 hebben geen betekenis, dus deze trekken we ervan af:

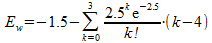
Dit kunnen we met een rekenmachine uitrekenen, ik kom op:

E_w$\approx$0,171

Dit is het gemiddelde aantal schepen dat per dag moet wachten.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 20 mei 2014