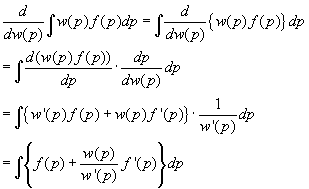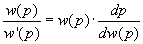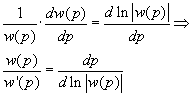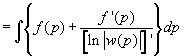|
|
|
\require{AMSmath}



Differentieren en integreren tegelijkertijd
Ik ben op zoek naar het volgende:
de partiele afgeleide naar w(p) van de integraal (w(p).f(p))
dus: d/dw(p) van integraal (w(p).f(p).dp), met als grenzen en max p en een min p.
Ik heb dit zelf geprobeerd met een formule van Euler. daarmee breng in de partieel afgeleide naar binnen in de integraal, en dan d/dw(p)van (w(p).f(p)), dit geeft f(p)
Dan schiet er nog over: de integraal van f(p).dp , en gegeven dat F'(p)=f(p), is dit dus gelijk aan F(p). Klopt dit ?
Annemi
Student universiteit België - zaterdag 11 januari 2003
Antwoord
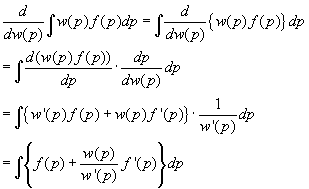
vervolgens maken we gebruik van:
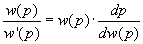
dit keren we om:
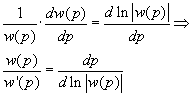
en vullen dit in:
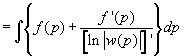
kom je hier iets verder mee?groeten,
martijn
mg
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 12 januari 2003
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|