|
|
|
\require{AMSmath}



Re: Oefening normale dichtheid: onbekende verwachte waarde ťn standaarddeviatie
Bedankt voor uw snel antwoord.
Ik begrijp de werkwijze en wat de bedoeling is. Maar ik heb toch nog een klein vraagje.
U schreef:"De z-waarde die hoort bij een kans van 0,9 (825 gram) is het tegengestelde van de kans 0,1."
Bedoelde u niet eerder dat de kans van 0,80 het tegengestelde is van 0,20? Natuurlijk zal deze regel ook wel gelden voor de percentages omtrent de 825 gram. Maar bij dat van 825 gram vragen ze naar 10% en dat valt nog af te lezen uit de tabel. Dus daar is dat niet echt van belang dacht ik zo.
Bij dat van X 800gram vragen ze echter naar de kans van een z-waarde van 80% en dat valt niet meer af te lezen uit mijn tabel. Dus enkel bij de vraag omtrent 800 gram zal ik uw stelling moeten toepassen toch? 800gram vragen ze echter naar de kans van een z-waarde van 80% en dat valt niet meer af te lezen uit mijn tabel. Dus enkel bij de vraag omtrent 800 gram zal ik uw stelling moeten toepassen toch?
Dus "De z-waarde die hoort bij een kans van 0,8 is het tegengestelde van de kans 0,2."
De kans van 0,2 heeft een z-waarde in mijn tabel van 0,84. Dus ik zie dat u in het stelsel inderdaad voor dat van 800gram -0,84 gebruikt.
Ik vraag mij alleen af waarom u net mag aannemen dat deze kansen elkaars tegengestelde zijn? Het is misschien een stomme vraag en ik vergeet waarschijnlijk iets essentieel. Maar ik zie niet echt waarom ze elkaars tegengestelde zijn. Ik was eerder aan het denken aan complementen.
Ik heb het stelsel ook uitgerekend, en ik bekom ook dezelde waarden voor m en s.
Nogmaals hartelijk bedankt voor uw hulp!
studen
Student universiteit BelgiŽ - woensdag 5 november 2008
Antwoord
De normale verdeling is een symmetrische verdeling. Dat betekent dat je 'feitelijk' aan een 'halve tabel' genoeg hebt.
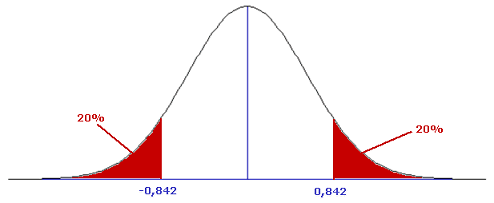
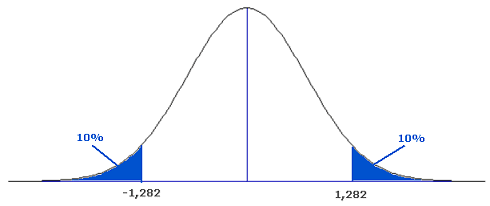
Hopelijk helpt dat...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 5 november 2008
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 57040
Dit is een reactie op vraag 57040  800gram vragen ze echter naar de kans van een z-waarde van 80% en dat valt niet meer af te lezen uit mijn tabel. Dus enkel bij de vraag omtrent 800 gram zal ik uw stelling moeten toepassen toch?
800gram vragen ze echter naar de kans van een z-waarde van 80% en dat valt niet meer af te lezen uit mijn tabel. Dus enkel bij de vraag omtrent 800 gram zal ik uw stelling moeten toepassen toch?


