|
|
|
\require{AMSmath}



Oefening normale dichtheid: onbekende verwachte waarde Ún standaarddeviatie
Probleemstelling:
Onderstel dat het gewicht van broden normaal verdeeld is met ongekende verwachte waarde en standaarddeviatie. We merken dat 20% van de broden minder wegen dan 800g en dat 10% meer wegen dan 825gram.
Wat is de verwachte waarde en standaarddeviatie van het gewicht?
Ik heb geprobeerd dit op te lossen via de normale dichtheid.
P(X 800) = 1 - P(X 800) = 1 - P(X 801) = 1 - P(Z 801) = 1 - P(Z 801 - m/s)= 0,20 801 - m/s)= 0,20
= 0,8 = P(Z 0,8 = P(Z 801 - m/s) 801 - m/s)
P(X 825) = P(Z 825) = P(Z 825 - m/s) 825 - m/s)
= 0,10
Ik heb een tabel van de standaardnormale dichtheid. Met P(Z z(a))=a z(a))=a
Maar daarin gaan de waarden voor z(a) maar tot 3,69 en de kansen dus maximaal tot 0,5000.
Uit de tabel heb ik kunnen afleiden dat
825 - m/s)= 1,28
Dus hieruit vind ik dat m= 825 -1,28s
Dus nu moet ik nog zoeken:
0,8 = P(Z 801 - 825 + 1,28s/s) 801 - 825 + 1,28s/s)
Maar voor waarde 0,8 is mijn tabel niet bruibaar.
Ik zit dus vast. Bovendien weet ik niet of ik wel met een goede oplossingsmethode bezig ben.(wij mogen geen grafisch rekentoestel hiervoor gebruiken, wel excel. wij hebben ook al verschillende andere soorten verdelingen, en kansvariabelen ed gezien..)
Alvast bedankt.
studen
Student universiteit BelgiŰ - woensdag 5 november 2008
Antwoord
Het idee is goed. De z-waarde die hoort bij een kans van 0,9 (825 gram) is het tegengestelde van de kans 0,1. Je hebt dan twee vergelijkingen met twee onbekende die je kan oplossen.
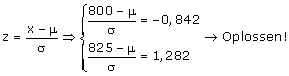
En als ik dan verder geen fout gemaakt heb zou m=809.9 en s=11.8 het antwoord moeten zijn.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 5 november 2008
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 800) = 1 - P(X
800) = 1 - P(X 801) = 1 - P(Z
801) = 1 - P(Z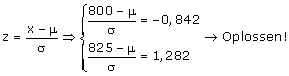


 Re: Oefening normale dichtheid: onbekende verwachte waarde Ún standaarddeviatie
Re: Oefening normale dichtheid: onbekende verwachte waarde Ún standaarddeviatie