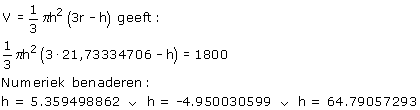WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Oplossen 3de graadsvergelijking

Dit is een reactie op vraag 48177

Bedankt voor de informatie !
Akkoord, ik kom 1 reële wortel (65,2) uit en 2 complexe wortels (ongeveer 0,2 + 5i en 0,2 -5i). Een algebraïsche 3de graadsvergelijking heeft altijd 3 wortels.
Maar dan is toch maar 1 fysisch resultaat, die 64 of 65 en dat kan toch niet ? hoe kan de hoogte van die bolkap groter zijn dan de straal van de grote bol ? Of moet ik het anders zien/begrijpen ?

De transformatie via Cardano leidt tot de vergelijking :
g² - 18812,1*g + 105379624 = 0
met g = u³
met u*v = p/3 en y = u-v (vergelijking wordt dan: y³+py+q=0)
met y = x + (b/(3a))
met p = (c-(b²/3a))/a
met q = ((2b³/(27a²))-(bc/3a)+d)/a
met h = x
vertekkende van -1,0472*hoogte³+68,2773*hoogte²-1800 = 0
of dus -1,0472x³ + 68,277x² - 1800 = 0
en dus de gedaante ax³ + bx² + cx + d =0 == c=0 in het vb

Mijn intuïtie/realisme zegt me dat ik iets rond de 6-8 meter moet uitkomen...

Graag uw visie aub.

Tom
Student Hoger Onderwijs België - woensdag 20 december 2006

Antwoord

Op Volume bolkap kan je een formule vinden:

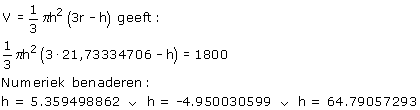
Dus... 3 reële oplossingen!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 20 december 2006