WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Integratie van een wortel som in de noemer

dx/(x¹/2+x¹/3)
zou moeten opgelost worden via substitutie tot:
2 x¹/2 - 3 x¹/3 + 6 x¹/6 - 6 ln | x¹/6 + 1 | + C

ik heb al op alle manieren geprobeerd om t= x¹/6 er in te passen maar ik kom er niet uit. moet het anders?
Wat moet ik gelijk stellen aan t?

Dominique
domini
Student Hoger Onderwijs België - dinsdag 13 december 2005

Antwoord

Beste Dominique,

Die substitutie is anders geen slecht idee, via x = t⁶ $\Leftrightarrow$ dx = 6t⁵ dt bekomen we dan de integraal:

$\int{}$6t⁵/(t³+t²) dt = $\int{}$6t³/(t+1) dt

Beschouw dan volgend truukje om de macht in de teller te verlagen:

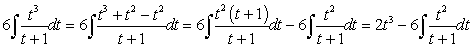
Hetzelfde kan je op die laatste integraal opnieuw toepassen, dit keer door '+ t - t'. Blijf zo de macht verlagen totdat deze 0 is in de teller, dan krijg je de verwachte ln van de uitdrukking in de noemer.

mvg,
Tom

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 13 december 2005