|
|
|
\require{AMSmath}



Construeren van hoeken van 84, 63 en 131 graden
hoe construeer je zonder een gradenboogje een hoek van 84, 63 (45+18) en 131 graden?
Steven
Leerling bovenbouw havo-vwo - maandag 14 maart 2005
Antwoord
Zonder gradenboog, maar wel met passer en liniaal (latje)?
Iets anders zou ik niet weten...
Wel, dan is een hoek van 131 graden niet met passer en liniaal (p & l) te construeren.
Want er geldt:
Van de gehele hoeken zijn ALLEEN die hoeken die een veelvoud zijn van 3°, met p & l construeerbaar.
Dus 84 en 63 zouden moeten kunnen!
Cruciaal bij deze constructies is de construeerbaarheid van een hoek van 72°.
En de constructie van een hoek van 72° is uitvoerbaar (met p & l), want je kan een regelmatige 5-hoek construeren (die heeft middelpuntshoeken van 72°).
En dan hebben we:
84 = 72 + (72 - 60)
en, zoals je zelf al aangeeft:
63 = 45 + 18 = 45 + 72 / 4
De constructie van een regelmatige 5-hoek is nogal ingewikkeld, en daardoor die van een hoek van 72° eveneens.
Hieronder staat zo'n constructie in 14 stappen.
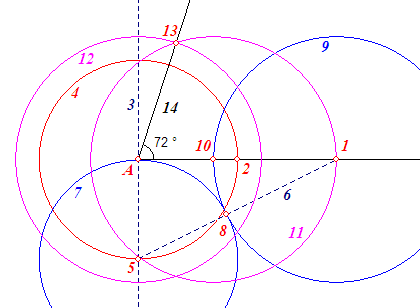
1 is een willekeurig punt op een lijn door A (het ene been van de hoek)
2 is het midden van A-1
3 is een loodlijn op A-1 in het punt A
4 is de cirkel met middelpunt A en straal A-2
5 is het snijpunt van 4 en 3
6 is het lijnstuk 5-1
7 is de cirkel met middelpunt 5 en straal 5-A
8 is het snijpunt van 7 en 6
9 is de cirkel met middelpunt 1 en straal 1-8
10 is het snijpunt van 9 en de lijn A-1
Het punt 10 verdeelt het lijnstuk A-1 volgens de gulden snede.
11 is de cirkel met middelpunt 10 en straal 10-1
12 is de cirkel met middelpunt A en straal 10-1
13 is een snijpunt van 11 en 12
14 is (uiteindelijk) het tweede been van de hoek van 72°
Zie voor het verband tussen de gulden snede en hoeken van 36° en 72° eventueel de onderstaande link.
Op die pagina staat ook de constructie van een regelmatige 5-hoek.
Oja, hoeken van 45° en 60° kunnen ook met p & l worden geconstrueerd.
Zie Gulden snede

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 15 maart 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










