Iets anders zou ik niet weten...
Wel, dan is een hoek van 131 graden niet met passer en liniaal (p & l) te construeren.
Want er geldt:
Van de gehele hoeken zijn ALLEEN die hoeken die een veelvoud zijn van 3°, met p & l construeerbaar.
Dus 84 en 63 zouden moeten kunnen!
Cruciaal bij deze constructies is de construeerbaarheid van een hoek van 72°.
En de constructie van een hoek van 72° is uitvoerbaar (met p & l), want je kan een regelmatige 5-hoek construeren (die heeft middelpuntshoeken van 72°).
En dan hebben we:
84 = 72 + (72 - 60)
en, zoals je zelf al aangeeft:
63 = 45 + 18 = 45 + 72 / 4
De constructie van een regelmatige 5-hoek is nogal ingewikkeld, en daardoor die van een hoek van 72° eveneens.
Hieronder staat zo'n constructie in 14 stappen.
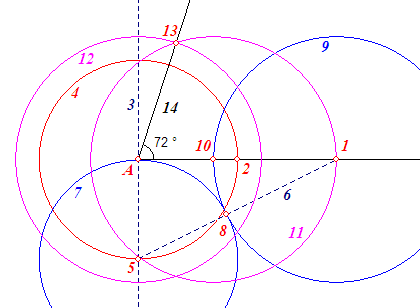
1 is een willekeurig punt op een lijn door A (het ene been van de hoek)
2 is het midden van A-1
3 is een loodlijn op A-1 in het punt A
4 is de cirkel met middelpunt A en straal A-2
5 is het snijpunt van 4 en 3
6 is het lijnstuk 5-1
7 is de cirkel met middelpunt 5 en straal 5-A
8 is het snijpunt van 7 en 6
9 is de cirkel met middelpunt 1 en straal 1-8
10 is het snijpunt van 9 en de lijn A-1
Het punt 10 verdeelt het lijnstuk A-1 volgens de gulden snede.
11 is de cirkel met middelpunt 10 en straal 10-1
12 is de cirkel met middelpunt A en straal 10-1
13 is een snijpunt van 11 en 12
14 is (uiteindelijk) het tweede been van de hoek van 72°
Zie voor het verband tussen de gulden snede en hoeken van 36° en 72° eventueel de onderstaande link.
Op die pagina staat ook de constructie van een regelmatige 5-hoek.
Oja, hoeken van 45° en 60° kunnen ook met p & l worden geconstrueerd.
Zie Gulden snede [http://www.pandd.demon.nl/sectioaurea.htm#23]
dk
15-3-2005