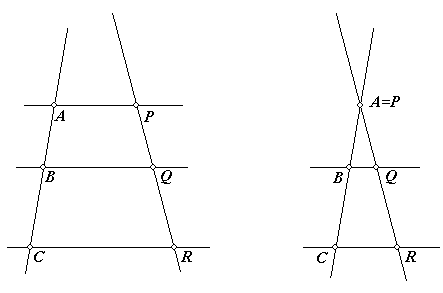|
|
|
\require{AMSmath}
Re: Stelling van Thales - evenwijdige projecties
Hallo
Is het niet mogelijk om het probleem te verklaren via deze stelling van Thales?
De lijnstukken afgesneden door // rechten op een snijlijn zijn evenredig met de overeenkomstige lijnstukken afgesneden op elke andere snijlijn.
Want hier op WisFaq gebruiken jullie Thales steeds in de context van driehoeken... Misschien een verschil bij Vlaanderen?
Omdat men in het handboek ook niet echt spreekt over driehoeken, maar gewoon over die stelling.
Ik weet niet of jullie hier een antwoord kunnen op vinden?
Evelie
2de graad ASO - donderdag 10 februari 2005
Antwoord
Laten we eerst een misverstand uit de weg ruimen...
In beide onderstaande figuren (links en rechts) is er sprake van "Thales". In de rechter figuur vallen de punten A en P samen. Meer niet (er is wat dit betreft echt geen verschil tussen Vlaanderen en Nederland)!
En natuurlijk kan je het krijgen zoals je het hebben wilt.
Ik volsta nu met een figuur,
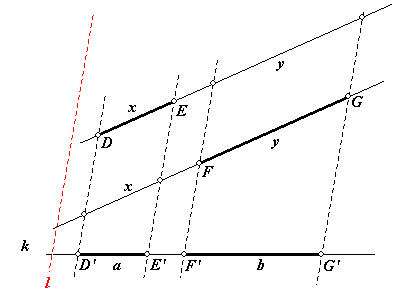
en de opmerking, dat hierin geldt:
x : y = a : b
(twee keer 'jouw' Thales toegepast?)
Ik vind het wel goed dat je even doorvroeg, want dit bewijs is eenvoudiger dan het vorige!
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 11 februari 2005
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 33897