WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Stelling van Thales - evenwijdige projecties

Hallo

In de meetkunde hebben we de stelling van Thales gezien:

De lijnstukken afgesneden door // rechten op een snijlijn zijn evenredig met de overeenkomstige lijnstukken afgesneden op elke andere snijlijn.

Deze stelling komt opnieuw aan bod bij het deel van evenwijdige projecties.

Via een onderzoek in het boek (projecties uitvoeren, lengten meten, verhoudingen bekijken) komt men tot hetvolgende besluit:

"Bij een evenwijdige pojectie zijn 2 lijnstukken evenredig met hun overeenkomstige beelden, ALS de DRAGERS van die lijnstukken EVENWIJDIG zijn".

Ik snap wel hoe men aan dit besluit komt wanneer de dragers van die 2 lijnstukken samenvallen (ik herken er dan de stelling van thales in).
MAAR ik ben dan niet meer mee wanneer de dragers van die lijnstukken evenwijdig zijn (dus niet samenvallen).

Het valt moeilijk te beschrijven zonder figuur...
Misschien hebben jullie het handboek? Het betreft wiskunde vandaag 3: meetkunde, uitgeverij Pelckmans.
Blz 110 - 111

Misschien een poging om de figuur te beschrijven:
-projectieas k, projectierichting l
-ze snijden elkaar
- drager [DE] // drager [FG], maar deze zijn niet evenwijdig met de projectieas
- bepaal de beelden van deze lijnstukken volgens de projectie: [D'E'] en [F'G'], deze liggen dus op de projectieas k.

Hoe vind je met Thales dat de verhouding (|DE|/|D'E'|) = (|FG|/|F'G'|)? Ik merk het wel door te meten, maar hoe vind je hier Thales in terug?

Hopelijk kunnen jullie helpen?
Evelie
2de graad ASO - donderdag 10 februari 2005

Antwoord

Allereerst, het boek heb ik niet. Dus wellicht had ik het beantwoorden beter aan een Vlaamse collega kunnen laten.
Maar ik waag toch een poging via onderstaande tekening.

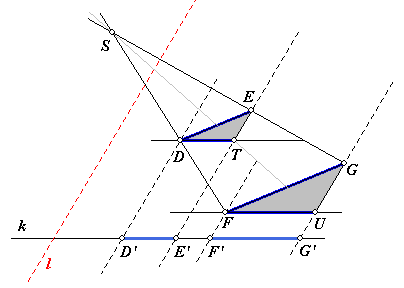
Door D en F zijn lijnen getekend evenwijdig met k.
Daardoor ontstaan de driehoeken DTE en FUG. Vanwege de evenwijdigheid van de overeenkomstige zijden van die driehoeken zijn ze gelijkvormig (zelfs homothetisch; zie het punt S).
En hier zit dan Thales... (eerst wat verstopt, maar nu duidelijk).

En dan kan je zelf wel verder, denk ik.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 10 februari 2005

Re: Stelling van Thales - evenwijdige projecties