Maar ik waag toch een poging via onderstaande tekening.
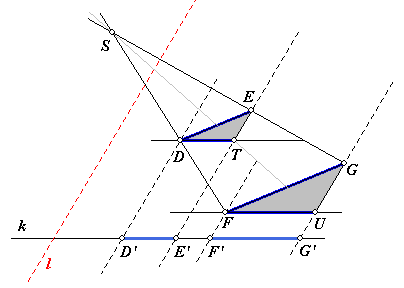
Door D en F zijn lijnen getekend evenwijdig met k.
Daardoor ontstaan de driehoeken DTE en FUG. Vanwege de evenwijdigheid van de overeenkomstige zijden van die driehoeken zijn ze gelijkvormig (zelfs homothetisch; zie het punt S).
En hier zit dan Thales... (eerst wat verstopt, maar nu duidelijk).
En dan kan je zelf wel verder, denk ik.
dk
10-2-2005