WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Oppervlakte tussen een parabool en een cirkel

Kunt U me aub even helpen:
bereken de oppervlakte van de figuur begrensd door y²=2x en de cirkel y²=4x-x².
Alvast bedankt.
karina
Student Hoger Onderwijs België - donderdag 17 juni 2004

Antwoord

Hoi,

Bekijk de volgende tekening.

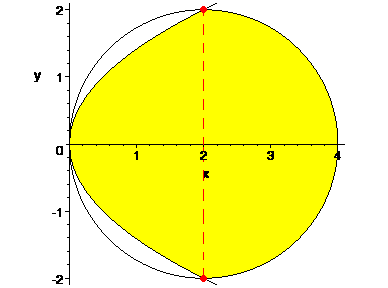
Het gele gebied is de gevraagde oppervlakte (dat is de "gemeenschappelijke" oppervlakte van de twee relaties).
Boven de x-as kun je de vergelijking van de halve cirkel als volgt opstellen g(x)=Ö(4x-x²) en de gedeeltelijke parabool heeft als functievoorschrift h(x)=Ö(2x). De functies worden in de x-as gespiegeld. Dus de oppervlakte boven de x-as is hetzelfde als de oppervlakte beneden de x-as. Bepaal het snijpunt van de twee functies (duidelijk is dat het punt (0,0) een snijpunt is). Dus g(x)=h(x)? Ö(4x-x²) = Ö(2x) Û 4x-x² = 2x Û 4x - 2x - x² = 0 Û -x² + 2x = 0 Û x(-x+2) = 0 Û x = 0 of x = 2.

De gemeenschappelijke oppervlakte op het interval [0,2] komt van de 'halve' parabool, dus ₀ò²Ö(2x)dx bepalen. Tip: Gebruik substitutie-methode óf splits Ö(2x) op in Ö(2)*Ö(x), maak gebruik van constante factor vóór integraalteken zetten, en Ö(x) = x^½ en dan de integreerregel voor exponenten òxⁿdx = ^xⁿ⁺¹/_{_n+1}. Op het interval [2,4] wordt de gemeenschappelijke oppervlakte door de halve cirkel bepaald, dus ₂ò⁴Ö(4x-x²)dx bepalen. Tip: Het is een kwart van de hele cirkel, oppervlakte van hele cirkel is 4p, dus een kwart hiervan is p. Dus de oppervlakte boven de x-as is de som van de bepaalde integralen. Maar de oppervlakte onder de x-as is precies hetzelfde, dus de totale oppervlakte boven de x-as (die heb je zojuist berekend) verdubbelen levert de oppervlakte van de beide relaties. De oppervlakte bedraagt ¹⁶/₃ + 2p.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 17 juni 2004