|
|
|
\require{AMSmath}
Scheermes van Ockham
Dit zou ik graag gebruiken voor een taak voor school, maar er is 1 bewijs waar ik de uitleg niet van weet.
-- het rekenkundig en het meetkundig gemiddelde van 2 positieve getallen.
zou u mij daarbij kunnen helpen?
groeten,
Leen V
Student Hoger Onderwijs België - dinsdag 6 april 2004
Antwoord
Ik voel niet meteen aan naar wat voor bewijs je precies op zoek bent. Laat ik het eens proberen met het volgende:
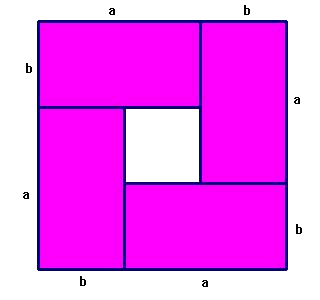
Het feit dat er een gat in de figuur zit, komt overeen met de gelijkheid
(a+b)2 = 4ab + (a-b)2
aangezien (a+b)2 de opppervlakte is van het grote vierkant, ab de oppervlakten van een rechthoek en (a-b)2 de oppervlakte van het gat. Zolang a en b verschillen is deze oppervlakte niet nul (en positief) zodat geldt
(a+b)2 4ab
(a+b)2/4 ab
[(a+b)/2]2 ab
(a+b)/2 Ö(ab)
en dit zijn precies de definities van de genoemde gemiddelden, zodat we hebben bewezen dat voor 2 verschillende positieve getallen steeds geldt
rekenkundig gemiddelde meetkundig gemiddelde
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 6 april 2004
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|
