|
|
|
\require{AMSmath}



Lineaire combinatie van vectoren in R2
Stel x = (−2, 3) en y = (7, 1). Hoeveel van de volgende vectoren zijn een lineaire
combinatie van x en y?
v1 = (5, 4), v2 = (11, −5) en v3 = (9, −2)
(A) 0
(B) 1
(C) 2
(D) 3
Het antwoord in de oplossingen is D.
". Enerzijds zien we dat x en y geen veelvoud zijn van elkaar, dus in R2 betekent dat dat ze samen het volledige vlak voortbrengen. Daaruit volgt dat alle vectoren uit R2 een lineaire combinatie zijn van x en y. "
Ik snap het gedeelte in haakjes niet zo goed, ik weet bijv niet hoe ik dit goed moet visualiseren.
Linh
Leerling bovenbouw havo-vwo - dinsdag 31 oktober 2023
Antwoord
Hallo Linh,
Als de vectoren x en y geen veelvoud van elkaar zijn, dan hebben zij verschillende richtingen, zoals in de onderstaande figuur. In dat geval kan elke vector in het vlak van x en y beschreven worden als de som van een aantal keer de vecor x plus een aantal keer de vector y (ofwel: een lineaire combinatie van x en y).
In het voorbeeld hieronder is de rode vector de som van de blauwe vector (een aantal keer x) en de groene vector (een aantal keer y).
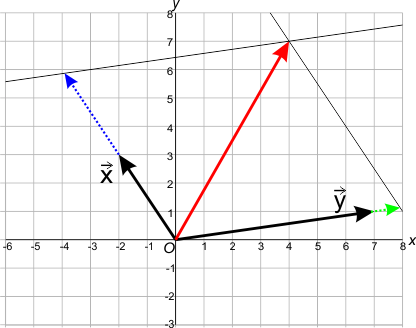
Dit lukt alleen wanneer de vecotoren x en y niet op één lijn liggen, ofwel: ze mogen geen veelvoud van elkaar zijn.
Kan je het nu wel voor je zien?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 31 oktober 2023
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|











 Re: Lineaire combinatie van vectoren in R2
Re: Lineaire combinatie van vectoren in R2