|
|
|
\require{AMSmath}



Inhoud cilinder met afgeplat onderzijde
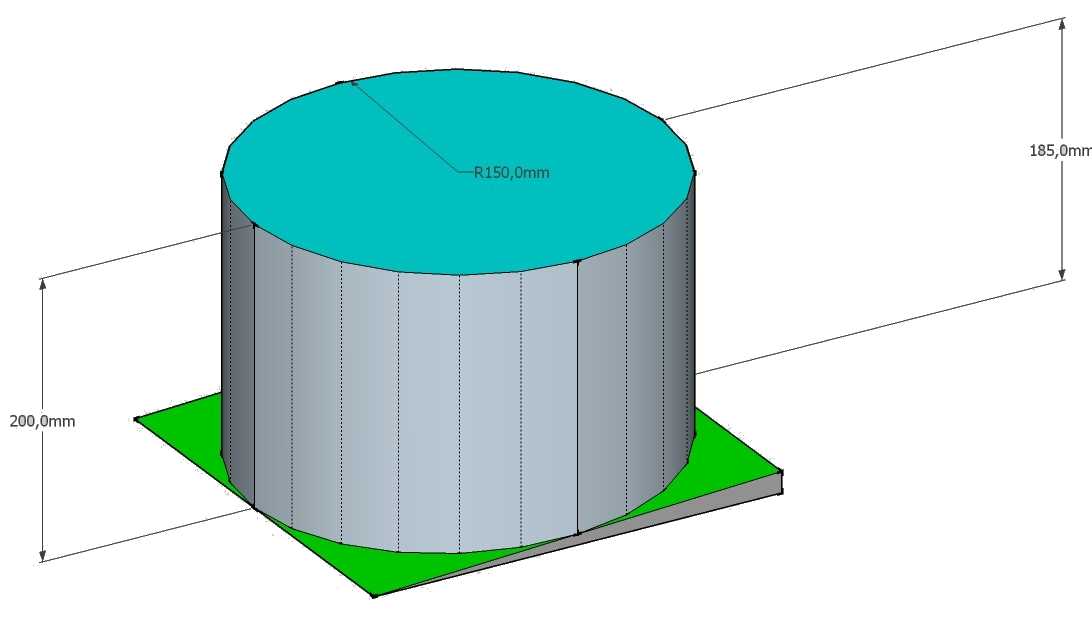
Ik zoek een inhoud berekening voor vloeistof in een verticale cilinder met een afgeplatte onderzijde. Met name de inhoud indien de bodem nog niet helemaal bedekt is.
Helling/afplatting 1:20
D = 300 mm (diameter cilinder)
H = 200 mm (vloeistofhoogte in de cilinder op laagste punt)
Ik ben dus op zoek naar het volume als functie van de hoogte.
Groet Jan
Jan
Iets anders - maandag 9 mei 2022
Antwoord
Laten we de cilinder zo draaien dat de lange lijnen in de tekening op/boven de $x$-as liggen en de centrale as op de $z$-as ligt. Dan heeft het grondvlak de (makkelijke) vergelijking $z=\frac1{20}(x+150)$.
De plak op hoogte $z\le15$ wordt dan bepaald door $x^2+y^2\le150^2$ Ťn $x\le 20z-150$.
De oppervlakte van zo'n plak is gelijk aan
$$\mathrm{Opp}(z)=\int_{-150}^{20z-150}2\sqrt{150^2-x^2}\,\mathrm{d}x
$$met behulp van een tabel of door partiŽle integratie vinden we dat de integraal gelijk is aan
$$\begin{aligned}
\left[x\sqrt{150^2-x^2}+150^2\arcsin\frac x{150}\right]_{-150}^{20z-150} & =
(20z-150)\sqrt{150^2-(20z-150)^2}\\
&\qquad{}+150^2\arcsin\frac{2z-15}{15}+150^2\cdot\frac\pi2
\end{aligned}
$$Het volume $V(h)$ is voor $h\le15$ dan gelijk aan
$$\int_0^h\mathrm{Opp}(z)\,\mathrm{d}z
$$met wat werk, of met behulp van tabellen, wordt dit
$$\begin{aligned}
V(h)&=\frac{150^2\pi}{2}h-\frac1{60}(150^2-(20h-150)^2)^{\frac32}\\
&\qquad{}+
\frac{15}2\times150^2\left(\frac{2h-15}{15}\arcsin\frac{2h-15}{15}+\sqrt{1-\left(\frac{2h-15}{15}\right)^2}+\frac\pi2\right)
\end{aligned}
$$Als $h=15$ krijgen we precies het volume van de cilinder met diameter $300$ en hoogte $15$, gedeeld door $2$, dus $V(15)=\frac12\pi\cdot150^2\cdot15$.
Voor $h\ge15$ hebben we
$$V(h)=V(15)+\pi\cdot150^2\cdot(h-15)
$$
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 12 mei 2022
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










 Re: Inhoud cilinder met afgeplat onderzijde
Re: Inhoud cilinder met afgeplat onderzijde