|
|
|
\require{AMSmath}



Tangens in een rechthoekige driehoek
Hallo,
Kan iemand mij aub zo snel mogelijk helpen?
Hoe bewijs ik het volgende? Het gaat om een rechthoekige driehoek ABC met rechte hoek in $\alpha$.
$
\eqalign{\tan \beta = \frac{{\sin \beta + \cos \gamma }}
{{\cos \beta + \sin \gamma }}}
$
Alvast bedankt!
Tim
2de graad ASO - woensdag 13 oktober 2021
Antwoord
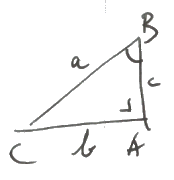 Er geldt: Er geldt:
$
\eqalign{
& \tan \beta = \frac{b}
{c} \cr
& \sin \beta = \frac{b}
{a} \cr
& \cos \gamma = \frac{b}
{a} \cr
& \cos \beta = \frac{c}
{a} \cr
& \sin \gamma = \frac{c}
{a} \cr}
$
Als je dat invult in $\eqalign{
\tan \beta = \frac{{\sin \beta + \cos \gamma }}
{{\cos \beta + \sin \gamma }}
}$ dan ben je er wel...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 14 oktober 2021
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Er geldt:
Er geldt:

