|
|
|
\require{AMSmath}



Re: Cirkel en raaklijn
Dag Klaas Pieter,
Dit is een grove fout van mij. Sorry .Onopletendheid blijkbaar...
Nu kom ik nu netjes bij de gevraagde waarden uit de waarden
x(1)=12 en x=-12 (a)
y(1)= 5 en y(2)=-5.(b)
a en b invullend in de gegeven vergelijking y=-Ī√(169-x2)= bekom ik netjes het 2 de lid van de vergelijking.( = 169).
De analytische kant van de zaak snap ik nu wel en had ik misschien beter gebruikt. Bedankt voor je keurig en mooi antwoord. Van
Mijnentwege zou ik zeggen Missen is menselijk . 'Tussen 169 en 25 is een groot verschil.
Groetjes en een leuke werkweek.
Rik Le
Iets anders - maandag 1 maart 2021
Antwoord
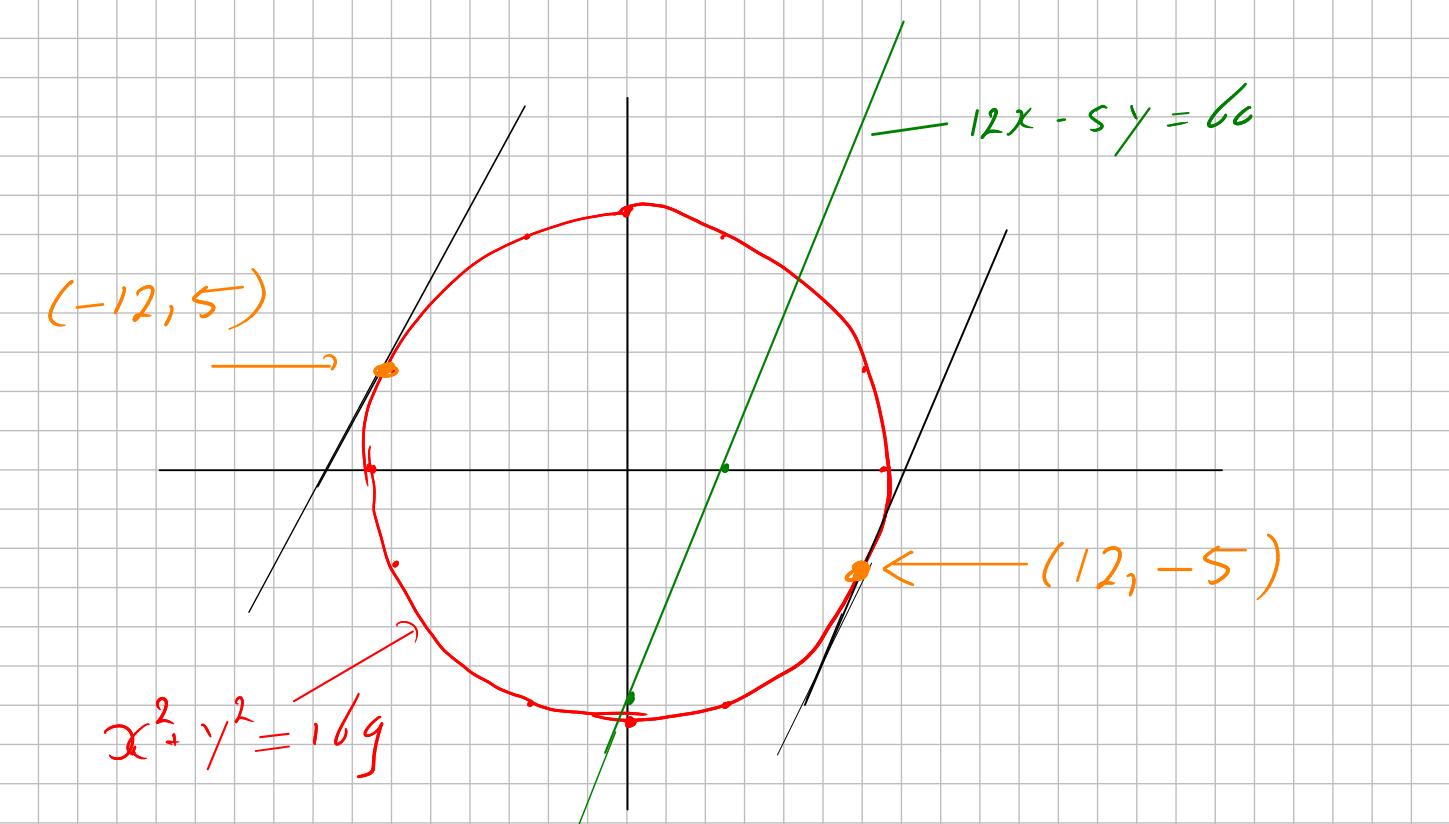
Niet helemaal: `mijn' methode levert de punten $(-12,5)$ en $(12,-5)$.
Je begon met de bovenste helft: $y=x/\sqrt{169-x^2}$ en dan moet $-x/\sqrt{169-x^2}$ gelijk zijn aan $12/5$ en dat betekent dat $-x$ positief moet zijn en $x$ dus negatief: $x=-12$, de $y$ is positief want we werken boven de $x$-as. De analytische methode geeft dus ook $(-12,5)$. En daarna ook $(12,-5)$.
Een tekening vooraf had je al in die richting kunen sturen.
kphart
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 1 maart 2021
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 91646
Dit is een reactie op vraag 91646 
