|
|
|
\require{AMSmath}



Eenheidscirkel
Hallo,
Als er gevraagd wordt: bereken met behulp van de eenheidscirkel, 10sin(alfa)+2=-3 hoe moet je dan te werk gaan?
dankuwel
Ramy O
Leerling bovenbouw havo-vwo - zondag 5 juni 2016
Antwoord
Hallo Ramy,
Eerst sin($\alpha$) isoleren:
10sin($\alpha$) + 2 = -3
10sin($\alpha$) = -5
sin($\alpha$) = -1/2
Als het goed is, weet je uit het hoofd:
sin(1/6$\pi$)=1/2
Dit teken je in de eenheidscirkel (in mijn tekening in het groen):
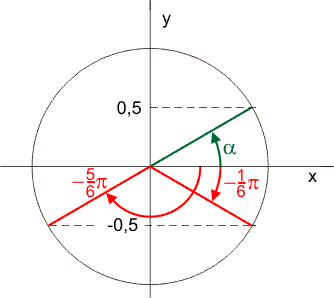
De sinus van hoek $\alpha$ lees je af op de y-as. Je wilt uitkomen op een waarde -1/2 in plaats van +1/2. In de eenheidscirkel zie je dat je dan 1/6$\pi$ 'achteruit' moet draaien, of 5/6$\pi$ 'achteruit'. Verder mag je natuurlijk een geheel aantal extra rondjes draaien, dus k·2$\pi$ radialen extra (k is een geheel getal).
Zodoende vind je:
$\alpha$ = -1/6$\pi$ + k·2$\pi$ radialen
of
$\alpha$ = -5/6$\pi$ + k·2$\pi$ radialen
OK zo?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 5 juni 2016
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










