WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vraagstuk aan de hand van een filmpje

Hoi,

Ik heb 2 filmpjes en ik heb hierbij 2 vragen die ik graag zou oplossen om te gebruiken in een simulatieprogramma dat ik zelf geschreven heb in C++. ( Ben informatica student )

Filmpje 1:

http://youtu.be/q6-9z5-huPA

Met daarbij als vraag: wat is de snelheid van het hoogste punt van de ladder?
Ik dacht hierbij aan misschien de afgeleiden te gebruiken maar indien ik aan de uitwerking begin loop ik steeds vast. Wiskunde is niet men beste vak.

Filmpje 2:

http://youtu.be/DqkDVfT8hDE

Met daarbij als vraag: wat is de snelheid van de top van de schaduw?
Hier heb ik geen idee om dit op te lossen.

Kan er mij hier iemand mee helpen alstublieft?
Alvast bedankt,
Bert
Student universiteit België - dinsdag 31 juli 2012

Antwoord

Beste,

Het eerste probleem wat je beschrijft is zeer bekend in de literatuur. Zoek maar eens op "Ladder rate-of-change problem". Ook op youtube zijn hier filmpjes van te vinden.

Mocht dat niet hetgeen zijn wat je zoekt, dan zou je het meer natuurkundig kunnen aanpakken:

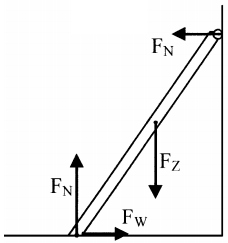
Het tweede probleem vind ik zelf zeer interessant/leuk.

Je hebt een voorwerp van x meter hoog.
Op een afstand van y meter heb je een lichtbron die voor een schaduw zorgt.
Als vervolgens de lichtbron met een snelheid van v m/s omhoog/omlaag gaat, groeit/krimpt de schaduw met w m/s.

Ik zou dit voor je kunnen uitrekenen, maar leukste is als je dit zelf doet.
Gewoon deze scenario's gebruiken:

- Schaduwlengte opschrijven
- Lamp 1 meter hoger zetten
- Schaduwlengte opschrijven
- Verschil van schaduwlengte uitrekenen
- Dit verschil delen door te tijd die de lamp nodig had om 1 meter hoger te komen.

Dit experiment paar keer herhalen (met andere waarden natuurlijk) en dan krijg je waarschijnlijk een indruk van de snelheid van de schaduw.

Natuurlijk zit het wiskundig wat ingewikkelder in mekaar, maar de "vrij standaard" natuurkundige formules kun je gewoon gebruiken.

Ik wens je veel succes toe met je programma in C++. Zelf ben ik een java-programmeur en kan je dus eventueel ook helpen als je vastloopt met je programma.

Laat alsjeblieft weten als je het opgelost hebt en ook graag hoe je het opgelost hebt.

Vriendelijk groetend,

PD

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 15 augustus 2012