|
|
|
\require{AMSmath}



Oppervlakte van een parallellogram
Gegeven:
oppervlakte driehoek MNB = 72cm2
lengte van AM = lengte van MB = lengte van MN
Gevraagd:
bereken de oppervlakte van het parallellogram.
Er is dus een driehoek getekend in het parallellogram ABCD, nl MNB. Punt N ligt op de basis DC en punt M daar rechtboven. Deze 2 punten zijn verbonden met elkaar d.m.v een rechte die loodrecht op AB en DC staat. Punt N is ook verbonden met hoek B. Zo ziet de driehoek in het parallellogram eruit.
bij voorbaat...
Romina
1ste graad ASO-TSO-BSO - zaterdag 7 februari 2004
Antwoord
Eerst maar eens tekening:
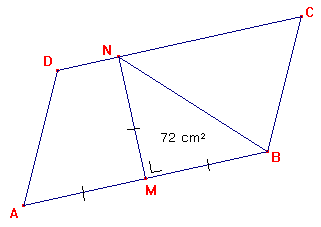
Zoals je ziet is –BMN een rechte hoek en BM=MN en AM=MB. Bereken de lengte van BM, MN en AM m.b.v. de oppervlakte van DBMN. De oppervlakte van het parallellogram is dan gelijk aan AB∑MN.
Zou dat lukken?

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 7 februari 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|










