Pot

Een vulapparaat deponeert jam in potten volgens een normale verdeling N(506,3). De grootte van glazen potten zelf is ook normaal verdeeld met N(512, 4).

• Hoe groot is de kans dat de jam bij het vullen niet in de glazen pot kan?

Zal u aub mij helpen met deze vraag.

R.
3de graad ASO - zondag 9 mei 2021

Antwoord

De inhoud van de pot noem ik I_pot met gemiddelde waarde $\mu$_pot=512 en standaarddeviatie $\sigma$_pot=4.
De hoeveelheid jam noem ik I_jam met gemiddelde waarde $\mu$_jam=506 en standaarddeviatie $\sigma$_jam=3.

Maak een nieuwe variabele V = I_pot-I_jam. Als V groter is dan nul, dan is de inhoud van de pot groter dan de hoeveelheid jam en past de jam in de pot. Als V kleiner is dan nul, dan is de inhoud van de pot kleiner dan de hoeveelheid jam en past de jam niet.

V is het verschil tussen twee normaal verdeelde variabelen I_pot en I_jam.. Dan is V ook weer normaal verdeeld met:

$\mu$_V = $\mu$_pot-$\mu$_jam
$\sigma$_V= √($\sigma$_pot²+$\sigma$_jam²)
(Let op het plus-teken bij de berekening van $\sigma$_V!).

Dus:
$\mu$_V = 512-506 = 6
$\sigma$_V= √(4²+3²) = 5

De vraag is dan:
Gegeven de normaal verdeelde variabele V met N(6 , 5). Hoe groot is de kans op een waarneming kleiner of gelijk aan nul (zie onderstaande figuur)?



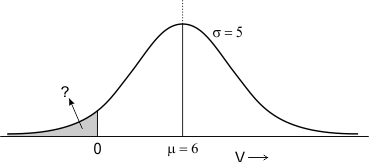
Ik kom op 11,5%. Jij ook?

maandag 10 mei 2021

©2001-2024 WisFaq