
Krommen
Beste
Ik zit vast in een oefening. Zal u aub mij daarbij helpen. Ik zal in de bijlage de vraag sturen. Ik heb geprobeerd om met verschilfunctie te werken maar het lukt niet.
Met vriendelijke groeten.
F.D
Fatima
3de graad ASO - vrijdag 16 april 2021
Antwoord
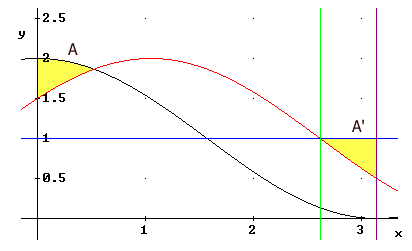
Je kunt de integralen uitwerken?
$
\eqalign{
& A. \cr
& \int\limits_0^{\frac{\pi }
{6}} {1 + \cos (x) - \left\{ {1 + \cos \left( {\frac{\pi }
{3} - x} \right)} \right\}} \,\,dx = \cr
& \int\limits_0^{\frac{\pi }
{6}} {\cos (x) - \cos \left( {\frac{\pi }
{3} - x} \right)} \,\,dx = \cr
& \left[ {\sin (x) + \sin \left( {\frac{\pi }
{3} - x} \right)} \right]_0^{\frac{\pi }
{6}} = \cr
& \sin \left( {\frac{\pi }
{6}} \right) + \sin \left( {\frac{\pi }
{3} - \frac{\pi }
{6}} \right) - \left\{ {\sin (0) + \sin \left( {\frac{\pi }
{3} - 0} \right)} \right\} = \cr
& \sin \left( {\frac{\pi }
{6}} \right) + \sin \left( {\frac{\pi }
{6}} \right) - \left\{ {\sin \left( {\frac{\pi }
{3}} \right)} \right\} = \cr
& \frac{1}
{2} + \frac{1}
{2} - \frac{{\sqrt 3 }}
{2} = \cr
& 1 - \frac{{\sqrt 3 }}
{2} \cr}
$
...en dan moet $A'$ dezelfde uitkomst geven:
$
\eqalign{
& A'. \cr
& \int\limits_{\frac{{5\pi }}
{6}}^\pi {1 - \left\{ {1 + \cos \left( {\frac{\pi }
{3} - x} \right)} \right\}} \,\,dx = \cr
& \int\limits_{\frac{{5\pi }}
{6}}^\pi { - \cos \left( {\frac{\pi }
{3} - x} \right)} \,\,dx = \cr
& \left[ {\sin \left( {\frac{\pi }
{3} - x} \right)} \right]_{\frac{{5\pi }}
{6}}^\pi = \cr
& \sin \left( {\frac{\pi }
{3} - \pi } \right) - \sin \left( {\frac{\pi }
{3} - \frac{{5\pi }}
{6}} \right) = \cr
& \sin \left( { - \frac{{2\pi }}
{3}} \right) - \sin \left( { - \frac{\pi }
{2}} \right) = \cr
& - \frac{{\sqrt 3 }}
{2} - - 1 \cr
& 1 - \frac{{\sqrt 3 }}
{2} \cr}
$
Dat zat er in, maar is dat een bewijs?

vrijdag 16 april 2021
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|