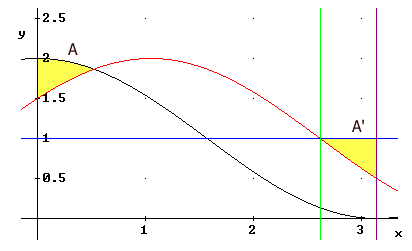
Je kunt de integralen uitwerken?
$
\eqalign{
& A. \cr
& \int\limits_0^{\frac{\pi }
{6}} {1 + \cos (x) - \left\{ {1 + \cos \left( {\frac{\pi }
{3} - x} \right)} \right\}} \,\,dx = \cr
& \int\limits_0^{\frac{\pi }
{6}} {\cos (x) - \cos \left( {\frac{\pi }
{3} - x} \right)} \,\,dx = \cr
& \left[ {\sin (x) + \sin \left( {\frac{\pi }
{3} - x} \right)} \right]_0^{\frac{\pi }
{6}} = \cr
& \sin \left( {\frac{\pi }
{6}} \right) + \sin \left( {\frac{\pi }
{3} - \frac{\pi }
{6}} \right) - \left\{ {\sin (0) + \sin \left( {\frac{\pi }
{3} - 0} \right)} \right\} = \cr
& \sin \left( {\frac{\pi }
{6}} \right) + \sin \left( {\frac{\pi }
{6}} \right) - \left\{ {\sin \left( {\frac{\pi }
{3}} \right)} \right\} = \cr
& \frac{1}
{2} + \frac{1}
{2} - \frac{{\sqrt 3 }}
{2} = \cr
& 1 - \frac{{\sqrt 3 }}
{2} \cr}
$
...en dan moet $A'$ dezelfde uitkomst geven:
$
\eqalign{
& A'. \cr
& \int\limits_{\frac{{5\pi }}
{6}}^\pi {1 - \left\{ {1 + \cos \left( {\frac{\pi }
{3} - x} \right)} \right\}} \,\,dx = \cr
& \int\limits_{\frac{{5\pi }}
{6}}^\pi { - \cos \left( {\frac{\pi }
{3} - x} \right)} \,\,dx = \cr
& \left[ {\sin \left( {\frac{\pi }
{3} - x} \right)} \right]_{\frac{{5\pi }}
{6}}^\pi = \cr
& \sin \left( {\frac{\pi }
{3} - \pi } \right) - \sin \left( {\frac{\pi }
{3} - \frac{{5\pi }}
{6}} \right) = \cr
& \sin \left( { - \frac{{2\pi }}
{3}} \right) - \sin \left( { - \frac{\pi }
{2}} \right) = \cr
& - \frac{{\sqrt 3 }}
{2} - - 1 \cr
& 1 - \frac{{\sqrt 3 }}
{2} \cr}
$
Dat zat er in, maar is dat een bewijs?

WvR
16-4-2021