Integreren

Integreren en breuksplitsen

Hallo wisfaq,

Ik wil graag de volgende integraal berekenen:

INT[1/((x⁴+1)(x⁵+1))]dx

Ik denk dat hier breuksplitsen toegepast kan worden maar ik weet niet zeker. Ik heb ook substitutie geprobeerd maar dat werkt niet.

Groeten,

Viky

• Integreren

viky
Iets anders - dinsdag 29 november 2016

Antwoord

Het kan op een paar manieren, maar elk is vrij veel werk. Het gaat in ieder geval wat makkelijker als je complexe getallen gebruikt.
1. Ontbind $x^4+1$ en $x^5+1=(x+1)(x^4-x^3+x^2-x+1)$ in lineaire factoren:
$$
x^4+1 = (x-e^{\frac\pi4i})(x-e^{-\frac\pi4i})(x-e^{\frac34\pi i})(x-e^{-\frac34\pi i})
$$
en
$$
x^4-x^3+x^2-x+1=(x-e^{\frac\pi5i})(x-e^{-\frac\pi5i})(x-e^{\frac35\pi i})(x-e^{-\frac35\pi i})
$$
2. Je kunt dit gebruiken om je breuk in negen eenvoudige termen van de vorm $A/(x-a)$ te splitsen en dan elke term te primitiveren; dat vergt nogal wat rekenwerk met complexe getallen. Het is dan nogal een werk om het antwoord dan weer reëel te maken.
3. Je kunt ook complex toegevoegde factoren weer vermenigvuldigen, dan komt er
$$
x^4+1 = (x^2-\sqrt2x+1)(x^2+\sqrt2x+1)
$$
en
$$
x^4-x^3+x^2-x+1=\left(x^2-2x\cos\frac\pi5+1\right)\left(x^2-2x\cos\frac35\pi+1\right)
$$
(er geldt $\cos\frac\pi5=\frac14+\frac14\sqrt5$ en $\cos\frac35\pi=\frac14-\frac14\sqrt5$).
Nu kun je gaan splitsen in vijf termen: $A/(x+1)$ en termen van de vorm $(Ax+B)/(x^2+ax+1)$. Ook dat is veel werk en dan krijg je een paar logaritmen en arctangensen in je primitieve.
Hier is het antwoord van Maple:

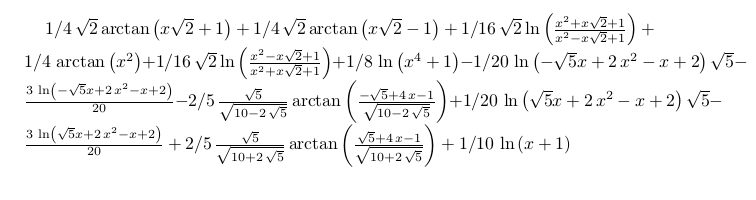
Zie Antwoord van Wolfram Alpha

kphart
dinsdag 29 november 2016

©2001-2024 WisFaq