De formule voor inhoud van een bolschijf

De vraag: Bewijs de formule voor inhoud van een bolschijf aan de hand van de integraalrekening.

Ik begin hieraan met een tekening waarbij ik de functie: y = wortel (r²- x²) opstel (r = straal) Deze wentel ik dan om de x-as. Het gaat over een bolschijf dus plaats ik links van de oorsprong punt B en rechts van de oorsprong punt A. Het gebied tussen deze 2 punten na de omwenteling is dan mijn bolschijf.

Dan bereken ik met de bepaalde integraal de inhoud: $\pi$ · integraal van b tot a van (r² - x²), maar hoe kom ik verder? Ik bereken een primitieve en los dit dan op, maar dan?

• Integreren

enya
3de graad ASO - dinsdag 3 juni 2014

Antwoord

Beste,

In principe is een bolschijf het volume van een bol tussen 2 grenzen a en b.
(zie plaatje)



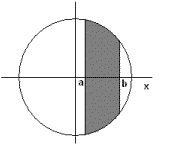
Je krijgt dan:
$
\pi \int\limits_a^b {r^2 - x^2 dx = \pi \left[ {r^2 x - \frac{1}{3}x^3 } \right]_a^b }
$

Maar stel dat je het volume van heel de bol wilt weten dan:
a=-r
b=r

Je krijgt dan:
$
\pi \int\limits_{ - r}^r {r^2 - x^2 dx = \pi \left[ {r^2 x - \frac{1}{3}x^3 } \right]_{ - r}^r }
$

Maar natuurlijk is het gemakkelijker om te kiezen voor:
a=0
b=r

En het volume voor de halve bol te berekenen, immers de hele bol is dan simpelweg het tweevoud ervan. Dus:

$
\begin{array}{l}
\pi \int\limits_0^r {r^2 - x^2 dx = \pi \left[ {r^2 x - \frac{1}{3}x^3 } \right]_0^r } \\
\pi (r^3 - \frac{1}{3}r^3 ) = \pi r^3 (1 - \frac{1}{3}) = \frac{{2\pi r^3 }}{3} \\
\end{array}
$

Voor de hele bol krijg je dan natuurlijk:

$
\frac{{4\pi r^3 }}{3}
$

mvg DvL

DvL
dinsdag 3 juni 2014

Re: De formule voor inhoud van een bolschijf

Re: De formule voor inhoud van een bolschijf

©2001-2024 WisFaq