Partieel integreren

ik heb hier een vraag over de volgende opgave, ik ga ergens de fout in, maar kan t niet vinden.

ò(lnx)/(x) dx

moet ik hier nu nemen voor
u=lnx du=dx/x
dv=dx/x v=lnx

maar dan krijg ik ... - ò(lnx)/(x) dx
dus daar schiet ik niets mee op

ofwel moet ik nemen
u=1/x du=lnxdx
dv=lnxdx v=xlnx-x

dit geeft dan
(xlnx-x)/(x) - ò(xlnx-x)lnxdx
en dat tweede deel krijg ik dan niet goed opgelost

zit daar een partiele integraal in een partiele integraal? dus dan
u=lnx du=dx/x
dv=(xlnx-x)dx v=(x²)/(2lnx)-x²/2

maar dit lijkt mij nogal raar uit te komen...

kunnen jullie me aub verder helpen?

bedankt!!!

Lien
Student universiteit België - donderdag 17 juli 2008

Antwoord

Ik denk dat 2. Substitutiemethode meer voor de hand ligt. Sterker nog: deze opgave staat er zelfs als voorbeeld.

Maar neem eens aan dat je 'denkt' dat partieel integreren de oplossing is. Je krijgt dan:



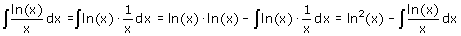
Dat lijkt niets, maar is toch wel 'grappig'. Er geldt:



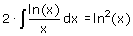
Maar dan:



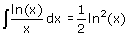
Zodat je er toch uitkomt...

donderdag 17 juli 2008

©2001-2024 WisFaq