Re: Diagonaalmatrix

Dit is een reactie op vraag 50547

Het is nu net die matrix P die ik niet kan vinden. P is toch de overgangsmatrix van de nieuwe gevonden basis van eigenvectoren naar de vorige basis die ik niet ken.

Je moet toch zoiets kunnen schrijven als:

(1,1)= x (?,?) + y (?,?)
(-2,1)= z (?,?) + w (?,?)

waaruit volgt dat P = (x z)
(y w)

In feite kan je ook de transformatie toepassen op deze eigenvectoren en hieruit dan de diagonaalmatrix halen? Maar ik veronderstel dat dit niet kan aangezien je de afbeelding niet kan achterhalen van deze vectoren.


Extra: In verband met jou opmerking van de eigenvector (-2,1) wat inderdaad correct is, kan je ook (2,-1) schrijven?

Pieter
Student Hoger Onderwijs België - dinsdag 1 mei 2007

Antwoord

Beste Pieter,

Een eigenvector is slechts bepaald op een constante factor (niet 0) na, dus ook (2,-1) is prima. Als geen andere basis gegeven is, gewoon ten opzichte van de standaardbasis, waarom zou je het moeilijker maken? In de kolommen van P staan dan gewoon de eigenvectoren. Dat levert:



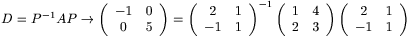
mvg,
Tom

dinsdag 1 mei 2007

Re: Re: Diagonaalmatrix

©2001-2024 WisFaq