Bissectrice bewijzen

Hallo,
Ik heb een probleempje met wiskunde. Ik moet bewijzen dat een bepaald lijstuk een bissectrie is van een hoek. Ik heb de tekening zelf al gemaakt, maar ik weet echt niet hoe ik verder moet. Ik denk dat ik de middelpuntshoek en de omtrekshoek moet gebruiken. Zouden jullie me een beetje op weg kunnen helpen?

Gegeven: cirkel (M,r), D is een punt van de cirkel; rechte AD raakt aan de cirkel. Een tweede rechte door A snijdt de cirkel in de punten B en C. OP AC nemen we het punt E zo, dat |AE|=|AD|(E ligt binnen de cirkel.

Te bewijzen: DE is de bissectrice van hoek BDC.

Ik weet dat het wel moelijk is om op deze vraag te antwoorden maar ik zou blij zijn als jullie me op weg zouden kunnen helpen.
Alvast bedankt!

Inkie
2de graad ASO - zaterdag 16 april 2005

Antwoord

Vergeet de middelpuntshoek, maar gebruik wel omtrekshoeken!!

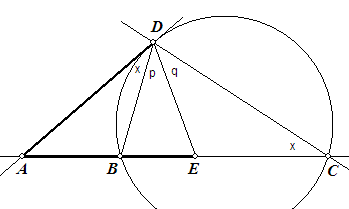
Ik heb wat letters in de hoeken gezet.
Te bewijzen is dan dat p = q.
Om je op weg te helpen wat vragen.
-- Waarom is hoek ADB = hoek BCD = x? Tip: zie boven.
Hoek BED is buitenhoek van driehoek ECD.
-- Wat weet je dan van die hoek?
-- Wat weet je van driehoek ADE?
-- En aan welke andere hoek is hoek BED dan ook gelijk?
-- Vind je nu ook dat x + p = x + q?

zondag 17 april 2005

Re: Bissectrice bewijzen

©2001-2024 WisFaq