
Som berekenen
beste wisfaq,
Hoe kan ik hieraan beginnen?
Bereken åvan n=0 tot ¥ (-1)^n/(3^n(2n+1))
Bereken åvan n=1 tot ¥ n/((n+1)!)
Is er een algemene formule om oneindige reeksen te bepalen?
groetjes van Fleur
Fleur
Student hbo - zondag 5 december 2004
Antwoord
dag Fleur
Een algemene formule is er niet, maar er zijn wel enkele hoopvolle routes aan te geven.
In jouw voorbeelden kun je mooi gebruik maken van Taylor-reeksen.
Op
MaclaurinSeries
vind je bijvoorbeeld:
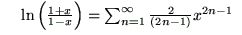
Vervang in deze formule de n door m+1, dus m = n-1 loopt van 0 tot ¥.
Dit lijkt al erg op de som die je moet berekenen, waarbij x gelijk is aan de wortel van -1/3, alleen mis je nog een factor 2, en nog een extra factor: de wortel uit -1/3.
Het resultaat zal (vanwege die wortel) dus complex zijn:
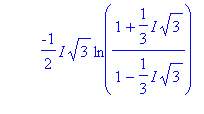
Voor de tweede som kun je gebruik maken van de Taylorreeks van de e-macht.
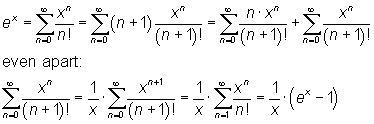
Vul nu voor x de waarde 1 in, en je kunt het antwoord op je vraag vinden.
groet,

woensdag 8 december 2004
 ©2001-2025 WisFaq
©2001-2025 WisFaq
|