|
|
|
\require{AMSmath}



Bereken k
De oppervlakte van het vlakdeel ingesloten door de grafiek van f met f(x)=x2-4x+3, de x-as, de y-as en de rechte met vergelijking x=k (k is een element van een reele getal R) is 4. Bereken k.
Ik heb het beetje gemaakt ma ik kom uit op k=4.82 terwijl ik volgens mijn boek 0.82 afwijk.
Kunt u kijken waarom ik zo een groot verschil heb?
Amber
3de graad ASO - woensdag 11 augustus 2021
Antwoord
Ik zou zeggen maak een tekening.
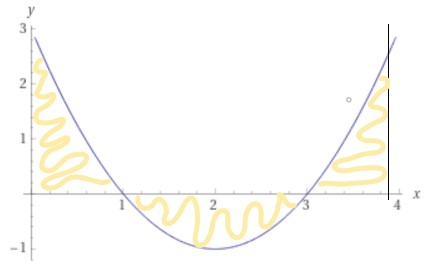
f(x) = x2-4x+3 = (x-1)(x-3) dus de grafiek snijdt de xas bij x=1 en x=3
Omdat het tweede gedeelte onder de x as loopt moet je die oppervlakte in 3 delen uitrekenen.
Namelijk van 0 tot 1 (11/3) van 1 tot 3 (11/3) en dan moet de oppervlakte van 3 tot k uitkomen op 4-11/3-11/3 = 11/3
En dan krijg ik uit k=4
Maar let op, dit is slechts de helft. Er is namelijk ook nog een negatieve waarde van k waarbij die oppervlakte op 4 uitkomt. Daarbij speelt die complicatie van het grafiekdeel onder de x-as niet.
Met vriendelijke groet
JaDeX

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 12 augustus 2021
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










