WisFaq!

Bereken k

De oppervlakte van het vlakdeel ingesloten door de grafiek van f met f(x)=x²-4x+3, de x-as, de y-as en de rechte met vergelijking x=k (k is een element van een reele getal R) is 4. Bereken k.

Ik heb het beetje gemaakt ma ik kom uit op k=4.82 terwijl ik volgens mijn boek 0.82 afwijk.

Kunt u kijken waarom ik zo een groot verschil heb?

Amber
11-8-2021

Antwoord

Ik zou zeggen maak een tekening.



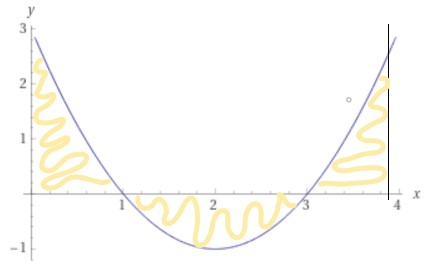
f(x) = x²-4x+3 = (x-1)(x-3) dus de grafiek snijdt de xas bij x=1 en x=3
Omdat het tweede gedeelte onder de x as loopt moet je die oppervlakte in 3 delen uitrekenen.
Namelijk van 0 tot 1 (1¹/₃) van 1 tot 3 (1¹/₃) en dan moet de oppervlakte van 3 tot k uitkomen op 4-1¹/₃-1¹/₃ = 1¹/₃

En dan krijg ik uit k=4

Maar let op, dit is slechts de helft. Er is namelijk ook nog een negatieve waarde van k waarbij die oppervlakte op 4 uitkomt. Daarbij speelt die complicatie van het grafiekdeel onder de x-as niet.

Met vriendelijke groet
JaDeX

jadex
12-8-2021