WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Zwaartepunt oppervlakte

De vraag is: Bepaal het zwaartepunt van het oppervlak begrensd door de gegeven krommen.

3y² = 4(3-x), x=0 antwoord: ($\frac{6}{5}$,0)

Deze oefening zit bij het deel 'zelfstudie' en ik er staat geen formule om dit te kunnen oplossen. Met welke formule los ik het op en hoe moet ik het toepassen met de formule?

Alvast bedankt!

Tugba
Student Hoger Onderwijs België - donderdag 16 januari 2014

Antwoord

Volgens Wikipedia kan je het zwaartepunt van een gebied onder de grafiek van een functie bepalen met:

$
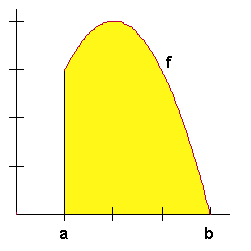
\Large\begin{array}{l}
x_Z = \frac{{\int\limits_a^b {x \cdot f(x)dx} }}{{\int\limits_a^b {f(x)dx} }} \\
y_Z = \frac{{\int\limits_a^b {\left( {f(x)} \right)^2 dx} }}{{2\int\limits_z^b {f(x)dx} }} \\
\end{array}
$

Bij jouw oefeninig kan je dat toepassen:

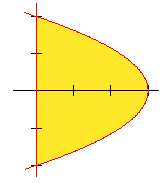
Ik zou dan $x$ uitdrukken in $y$ en proberen $x_Z$ en $y_Z$ te bepalen.
Zou dat lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 16 januari 2014

Re: Zwaartepunt oppervlakte