WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Volume mbv drievoudige integraal

Geachte

Mijn opgave luidt als volgt: Bereken het volume tussen het xy-, xz- en yz)vlak en het vlak x + 2y + 3z = 6.

De oplossing dient te zijn: ò_[0,6]ò_{[0, 3 - ^x/₂]}ò_{[0, ^{6 - x - 2y}/₃]}dzdxdy

De weg hiernaartoe vind ik niet. Eventueel had ik het volgende uitgedokterd:
* z=(6 - x - 2y)/3 en laat de integraal voor dz van o tot de waarde rechts in dit lid lopen
* stel deze waarde nu gelijk aan 0, dan is 6 - x - 2y = 0 en is y = (6 - x)/2 en laat de integraal voor dy van 0 tot de waarde rechts in dit lid lopen
*stel deze waarde nu gelijk aan 0, dan is 6 - x = 0 en is x = 6 en laat de integraal voor dx van 0 tot 6 lopen

Echter, dan is de volgorde van differentialen in de integraal van mijn einduitkomst niet dzdxdy, maar dzdydx.

Enig idee hoe dit komt?

M.v.g.

Brecht
Brecht
Student universiteit België - zondag 4 januari 2009

Antwoord

In het xy-vlak geldt z=0. De niveaulijn heeft de vergelijking x+2y=6. Als je x laat lopen van 0 tot 6, dan loopt y van 0 tot -¹/₂x+3. In dat geval loop z van 0 tot -¹/₃x-²/₃y+1. Dus om de inhoud te berekenen krijg je:

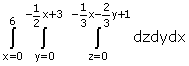
..en dat zou verder geen probleem mogen zijn. Wat je schrijft bij 'de oplossing dient te zijn' lijkt me dus niet juist. Lijkt me een verschrijving.

Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 4 januari 2009