|
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
|||||||||||||||||
|
\require{AMSmath}



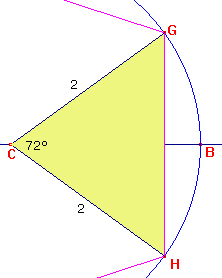
Constructie van een regelmatige vijfhoekWe gaan deze constructie uitvoeren. Neem eens aan dat we een lijnstuk AB met C al in twee delen hebben verdeeld en wel volgens de Gulden Snede. Teken nu een cirkel g om C met straal BC. We gaan de vijfhoek construeren in de cirkel g. g Snijdt het verlengde van lijnstuk AB in D. Dit punt D is al een van de punten van de vijfhoek die we zoeken. Teken nu een cirkel om A met straal BC. Deze cirkel snijdt g in twee punten E en F. Ook dit zijn punten van de vijfhoek. Je hebt nu al drie punten van de vijfhoek gevonden. Heb je enig idee hoe je de andere twee vindt? Antwoord



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2024 WisFaq - versie 3
| |||||||||||||||||