Als je bij een telprobleem steeds een keuze gemaakt moet worden uit twee alternatieven, dan ontstaat er een zeer regelmatig wegendiagram. We noemen zo'n wegendiagram een roosterdiagram. Het ziet er uit als roosterpapier.
Voorbeelden van een keuze tussen twee alternatieven:
-
jongen/meisje
-
winnen/verliezen
-
noord/oost
-
kop/munt
Voorbeeld 1
-
Een gezin heeft 5 kinderen. Op hoeveel verschillende manieren kan het gezin zijn samengesteld?
Dit kan op 25 = 32 manieren.
Als je niet op de volgorde let, zijn er 6 verschillende samenstellingen mogelijk. Hierbij gebruik je de driehoek van Pascal.
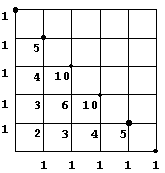
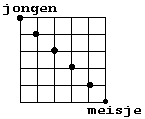
Elk volgend getal kun je uitrekenen door de getallen waar je vandaan kan komt op te tellen. Als je naar rechts gaat is het een meisje en als je naar boven gaat is het een jongen.
Je kunt nu allerlei vragen beantwoorden:
-
Wat is de kans dat een gezin met 5 kinderen bestaat uit 2 meisjes en 3 jongens?
-
Wat is de kans op een gezin met 5 kinderen met alleen jongens of alleen meisjes?
-
Wat is de kans dat er bij een gezin met 5 kinderen meer meisjes dan jongens zijn?
Antwoorden
-
\large\frac{10}{32}=\frac{5}{16}
-
\large\frac{2}{32}=\frac{1}{16}
-
\large\frac{16}{32}=\frac{1}{2}
Voorbeeld 2
-
Bij een voetbalwedstrijd was 1-1 de ruststand en de eindstand was 4-3. Hoeveel verschillende wedstrijdverlopen zijn er mogelijk?
Hieronder zie je alle mogelijke spelverlopen in een roosterdiagram. Je kunt daarin zien hoe je van (0,0) naar (4,3) kan komen met een ruststand van (1,1). De rode getallen geven het aantal doelpunten weer en de blauwe getallen het aantal manieren om in een bepaald punt te komen.
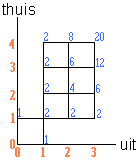
Het antwoord is dus 20.
Dit kan je ook uitrekenen. De punten in zo'n roosterdiagram komen overeen met het aantal combinaties. In dit voorbeeld:
N={2\choose1}\cdot{5\choose2}=20
of
N={2\choose1}\cdot{5\choose3}=20
Kijk even goed waar de 5 boven 2 (en 5 boven 3) vandaag komt. Je hebt van (1,1) naar (3,4) in totaal 5 stappen, hierbij kies je 2 keer voor uit en 3 keer voor thuis!
Voorbeeld
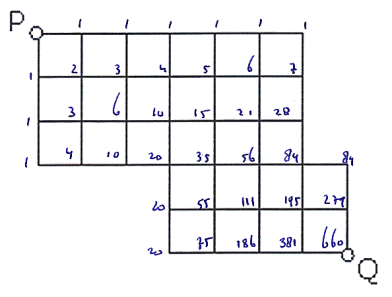
Hieronder zie je een roosterdiagram. Hoeveel kortste routes zijn er van P naar Q?
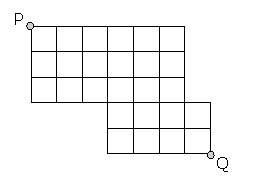
..en dat is dan een kwestie van tellen! Kijk maar 's goed:
F.A.Q.

