WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

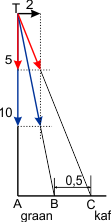
Vergelijkingen

Graan van kaf scheiden

Men wil graandeeltjes naar grootte scheiden van kafdeeltjes. Uit proeven is gebleken dat de graankorrels een bezinksnelheid hebben tussen 10 en 15m/s. De kafdeeltjes hebben een bezinksnelheid tussen 2 en 5m/s. Men laat daartoe alles vallen door een scheidingsapparaat. Deze heeft bovenaan een 80 cm brede spleet. Daaronder is er een horizontale luchtstroom met een snelheid van 2m/s. Men wenst een scheidingszone van 5dm tussen de neerslaggebieden te handhaven.
Bereken de hoofdafmetingen van het apparaat.

Arnold
4-1-2025

Antwoord

Hallo Arnold,

Ik begrijp dat aangenomen mag worden dat graandeeltjes en kafdeeltjes met een horizontale snelheid van 2 ^m/_s worden meegenomen door de luchtstroom. Dan wordt de breedte van de scheidingszone bepaald door de langzaamste graandeeltjes (deze worden het verst meegenomen) en de snelste kafdeeltjes (deze worden het minst ver meegnomen).
Maak dan eerst een schets waarin je de richting aangeeft waarin deze langzaamste graandeeltjes en snelste kafdeeltjes vallen:

De graandeeltjes vallen 10 meter per 2 meter horizontale verplaatsing (blauw). In driehoek ABT geldt dan:
^AB/_AT = ²/₁₀.

Voor de kafdeeltjes is dit 5 op 2 meter (rood). In driehoek ACT levert dit:
^AB+0,5/_AT = ²/₅.

Je hebt nu 2 vergelijkingen met 2 onbekenden. Los dit stelsel op om AT (=hoogte van de installatie) en AB te berekenen. AC is dan ook bekend (AB plus de breedte van de scheidingszone), je weet dus de minimale breedte van de installatie.

De vraag is allen nog of de langzaamst vallende kafdeeltjes de grond moeten bereiken, of dat deze ook tegen de rechter wand 'geblazen' mogen worden. Als deze vrij moeten kunnen vallen, moet je nog een gelijksoortige berekening maken om de breedte van de installatie te bepalen.
GHvD
5-1-2025

Vergelijking

Gegeven: x^x =√2/2 . bepaal x algebraïsch,ik heb het al geprobeerd en ik kwam alleen maar ¹/₂ uit maar er is blijkbaar nog een tweede oplossing nl. 1/4,hoe kan je hiertoe komen?l
Bert
22-1-2025

Antwoord

Als je grafiek van $x^x$ plot voor $0\le x\le 1$ zie je dat er veel $y$-en tussen $0$ en $1$ zijn met twee oplossingen voor $x^x=y$. Die vind je door proberen, daar is geen mooie formule voor.

In dit geval zou je die oplossing kunnen vinden als je bedenkt dat $4^{\frac14}=2^{\frac24}=\sqrt2$, en dus $(\frac14)^{\frac14}=\frac1{\sqrt2}$. Maar voor bijna alle andere waarden heb je niet zoveel geluk.
kphart
22-1-2025

Vergelijking

De vergelijking sqrt(x²-1) $>$ -x zou je makkelijk kunnen oplossen met een tekentabel, maar er is nog een andere oplossingsmethode,sqrt(x²-1) is een parabool, zitten we aan de stijgende of dalende kant dan keert het teken (wel) om... Hoe werkt dit precies?
Pieter
28-1-2025

Antwoord

Om te beginnen: de grafiek van $y=\sqrt{x^2-1}$ bestaat uit de helften van de hyperbool met vergelijking $x^2-y^2=1$ die boven de $x$-as liggen. Dus, nee, het is geen parabool.

Iets makkelijken: $\sqrt{x^2-1}$ is kleiner dan $\sqrt{x^2}$ en dat is weer gelijk aan $|x|$. Dus als $x$ negatief is heb je $\sqrt{x^2-1} < |x|=-x$.
Verder, als $x$ positief is geldt $\sqrt{x^2-1} \ge0 > -x$.
NB de uitdrukking is alleen geldig als $|x|\ge1$.
kphart
28-1-2025

Homogene vergelijking in sinx en cosx

Beste wisfaq, als deze vergelijking gegeven is 8 sin⁴x + 22 cos⁴x – 15 sin x cos x = 0 Dit is bijna een homogene vergelijkingk, dus ik dacht om de laatse term de vermenigvuldigen met 1 en dan krijg je na een aantal stappen het volgende (na subsitutie) 8t⁴ -15t³ -t+22=0 maar als ik naar de grafiek kijk heeft hij geen nulwaarden en bij de oplossingen staat dat hij wel nulwaarden heeft, zouden jullie mij kunnen zeggen waar ik fout ben?
Groeten, Julien.
Julien
23-2-2025

Antwoord

Helaas, nee.

Je hebt het belangrijkste weggelaten: waar staat de $t$ voor in $8t^4-15t^3-t+22$?

Ik heb gekeken wat er gebeurt als je $\sin x$ of $\cos x$ voor $t$ invult, en beide resultaten zijn ongelijk aan de gegeven functie van $x$.

Je moet bij dat vermenigvuldigen een fout gemaakt hebben, maar zo kunnen we niet zien welke.
kphart
23-2-2025