Driehoek met omschreven cirkel

Gevraagd:

Beschouw een gelijkzijdige driehoek ABC met zijde 1. Laat M het middelpunt zijn van de cirkel omschreven rond deze driehoek. Laat punt D het beeld zijn van punt B na muntspiegeling rond M. Wat is de afstand van A tot D?

Wat ik heb geprobeerd:

Door de situatie te schetsen kreeg ik de indruk dat de driehoek ABD te verkrijgen is door punt C te schuiven langs de cirkel tot de positie van punt D, tevens is de afstand BD gelijk aan de diameter van de cirkel. Verder dan dit kom ik helaas niet...

Leerling bovenbouw havo-vwo - zondag 26 mei 2024

Antwoord

Hallo Erik-Jan,

Prima om een schets te maken:



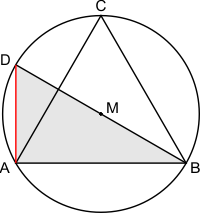
Bekijk driehoek ABD met hoeken 90°, 30° en 60°. De zijden verhouden zich als 1:2:√3. Je weet: AB=1, dus met deze verhoudingen is zijde AD te berekenen.

Lukt het hiermee?

zondag 26 mei 2024

©2004-2024 WisFaq