Tweedegraadsvergelijking oplossen zonder discriminant
Beste,
Volgende vergelijking moet ik oplossen zonder gebruik te maken van de discriminant"
-(x+7)2 -5 =0
Kan je me helpen? Zelf heb ik de oplossing al verder uitgewerkt naar x2+14x+54=0, vervolgens wou ik deze splitsen in factoren naar de vorm (x+p)(x+q)=0, waarbij p·q= 54 en p+q=14. Maar ik vind geen waarden voor p en q waarvoor deze voorwaarden gelden.
Bedankt alvast
3de graad ASO - woensdag 24 april 2024
Antwoord
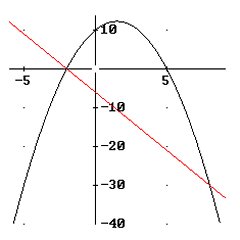 Dit is een voorbeeld is van een tweedegraadsvergelijking waarbij er een kwadraat is afgesplits. Je kunt zo'n vergelijking zo oplossen:
$
\eqalign{
& - (x + 7)^2 - 5 = 0 \cr
& - (x + 7)^2 = 5 \cr
& (x + 7)^2 = - 5 \cr
& {\text{geen}}\,\,\,{\text{oplossing}} \cr}
$
Geen oplossing is dit geval. Op Meer voorbeelden... kan je voorbeelden vinden hoe zoiets er uit ziet als er wel een oplossing is:
woensdag 24 april 2024
©2004-2024 WisFaq
|