Newton en Raphson

Wat houdt de methode voor differentiëren van Newton en Raphson in. En hoe kan ik de formules afleiden met een plaatje?

v.
Leerling bovenbouw havo-vwo - donderdag 20 februari 2003

Antwoord

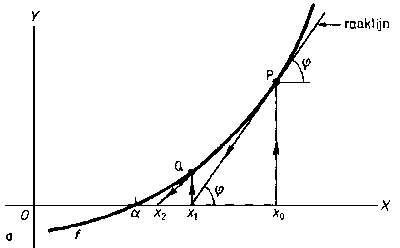
De werking van de methode van Newton-Raphson blijkt uit het bovenstaand plaatje. We zoeken het nulpunt $\alpha$ van een bepaalde functie. Kies punt P ergens op de grafiek.
De x-coordinaat van P is x₀ de y coordinaat is f(x₀)
De raaklijn in P heeft rico f'(x₀)=tan $\phi$
Nu geldt tan $\phi$= f'(x₀) = f(x₀)/(x₁-x₀)
Hierbij is x₁ een punt dat dichter bij het gezochte snijpunt met de x-as ligt dan x₀.
Omrekenen levert een formule: x₁=x₀-(f(x₀))/(f'(x₀))
En zo is de volgende waarde: x₂=x₁-(f(x₁))/(f'(x₁))

Newton Raphson wordt dus niet gebruikt om te differentiëren maar om met behulp van differentiëren nulpunten te benaderen.

Laten we eens kijken of we √2 zo kunnen berekenen.
Welnu √2 is nulpunt van f(x) = x²-2 dan f'(x)=2x

Neem nu als eerste benadering x₀=1,6 deze waarde is natuurlijk veel te groot !
Dan wordt x₁=x₀-(f(x₀))/(f'(x₀))=1,6-((1,6²-2)/(2·1,6))=1,425
vervolgens x₂=1,425-((1,425²-2)/(2·1,425))=1,4142544

bereken nu x₃ zelf eens en vergelijk het resultaat met √2 op je rekenmachine

Bingo !

Met vriendelijke groet

JaDeX

vrijdag 21 februari 2003

Re: Newton en Raphson

©2001-2024 WisFaq