Een raaklijn door de oorsprong

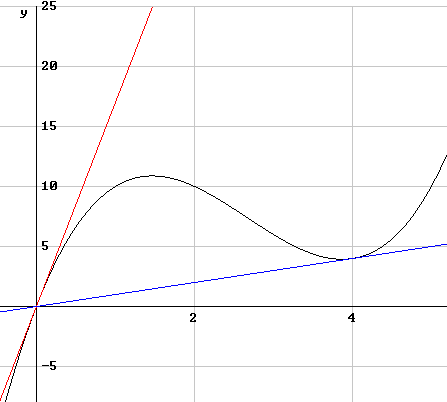
De vraag luidt: In welke punten van de grafiek van de kromme met vergelijking y = x³ - 8x² + 17x gaat de raaklijn door de oorsprong? Zelf kom ik nog tot het bepalen van de afgeleide.
y' = 3x² - 16x + 17. Verder heb ik geen idee, wie helpt?

Solido
Student hbo - woensdag 7 mei 2014

Antwoord

Een lijn door de oorsprong heeft als vergelijking $y=ax$. Als je de lijn snijdt met de kromme en eist dat je één snijpunt krijgt?

Eén raaklijn kan je al meteen zien: $y=17x$ voor $x=0$.

Voor $x\neq 0$ stel je $ax$ gelijk aan $x^3-8x^2+17x$, los de vergelijking op en eis dat er slechts één snijpunt is (raaklijn!). Iets met de discriminant?

Zou dat lukken?

woensdag 7 mei 2014

Re: Een raaklijn door de oorsprong

©2001-2024 WisFaq