WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

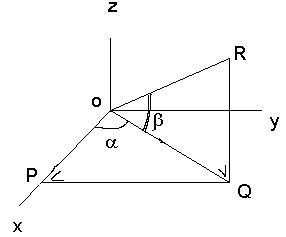
Samengestelde hoeken

Indien een hoek wordt gedefinieerd door een verdraaiing in het horizontale vlak tezamen met een (andere) verdraaiing in het verticale vlak, hoe bereken je dan snel (formule) de waarde van de samengestelde hoek?
maarte
Iets anders - dinsdag 15 april 2003

Antwoord

Stel |OP|=1, dan is |PQ|=tg(a) en |OQ|=1/cos(a).
Daaruit volgt dan weer dat |OR|=1/[cos(a)cos(b)] en |QR|=tg(b)/cos(a).

Gebruik nu Pythagoras in driehoek PQR

|PR|²=|PQ|²+|QR|²

de cosinusregel in driehoek OPR (met g de gevraagde hoek POR)

|PR|²=|OP|²+|OR|² - 2|OP||OR|cos(g)

en de identiteit

tg²(x) = 1/cos²(x) - 1

en je bekomt de mooie formule

cos(g) = cos(a) cos(b)

Afgaand op het resultaat kon het misschien eenvoudiger...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 15 april 2003