WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Wentelen om y-as van een NIET-functie

Dit is een reactie op vraag 98537

Geachte,
Hartelijk dank voor uw snelle antwoord. Voor alle duidelijkheid: er moet toch gewenteld worden om de y-as (Sorry voor het foutje in mijn vraag...)

De opdracht was om het 'begrensde' gebied te wentelen om de y-as. (Ik ging uit van de 2 gebieden in de 2 'waterdruppels'; ik zie niet welke andere gebieden er anders bedoeld zouden zijn) Het antwoord zou 64/105 $\pi$ zijn volgens het antwoordblad...

Waarom kan ik niet gewoon x en y verwisselen en dan gebruiken x²=y²-y³? Maar hoe zit het dan met de grenzen???

Nogmaals hartelijk dank!
Dian
Leerling bovenbouw havo-vwo - vrijdag 21 februari 2025

Antwoord

Het verwisselen van $x$ en $y$ betekent dat je het gebied spiegelt in de lijn $y=x$, en als je dat doet moet je dat gebied om de $x$-as draaien en dat betekent dat je de vergelijking naar $y$ moet oplossen, met dezelfde ingewikkelde formule als resultaat.

De opgave wordt een stuk makkelijker door poolcoördinaten te gebruiken. We voeren even een derde coördinaat $z$ in en drukken de kromme uit in $x$ en $z$ door $z^2=x^2-x^3$. Als de die om de $z$-as (die staat loodrecht op het $xy$-vlak) draaien. Je krijgt dan dit:

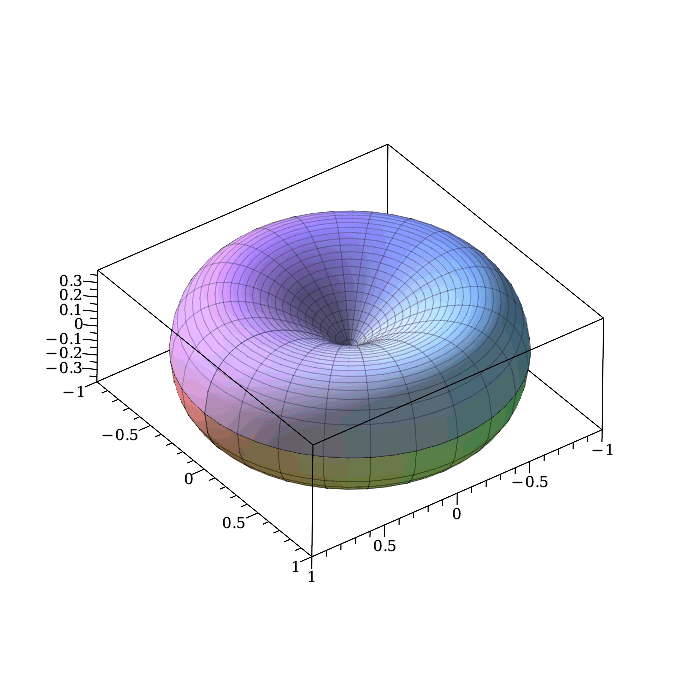
De vergelijking van het oppervlak is dan $z^2=(x^2+y^2)-(x^2+y^2)^{\frac32}$, en in poolcoördinaten wordt dat $z^2=r^2-r^3$ (want $x=r\cos\theta$, en $y=r\sin\theta$).
In de beschrijving loopt $\theta$ helemaal rond: $0\le\theta\le2\pi$, en voor $r$ geldt $0\le r\le1$, en voor $z$ komt er $-\sqrt{r^2-r^3}\le z\le\sqrt{r^2-r^3}$.
De inhoud van het wentellichaam wordt dan
$$
2\pi\cdot\int_0^12\sqrt{r^2-r^3}\cdot r\,\mathrm{d}r
$$
Omdat $r$ positief is kun je er deze integraal van maken: $4\pi\int_0^1r^2\sqrt{1-r}\,\mathrm{d}r$ en die levert inderdaad het antwoord dat je noemt.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 22 februari 2025