WisFaq!

Loading jsMath...

De digitale vraagbaak voor het wiskundeonderwijs

HOME

\require{AMSmath}

Re: Integreren met een limiet

Dit is een reactie op vraag 98406

Als ik bij (1-x \sqrt{} x)ln(1- \sqrt{} x) voor x=1 invul zou er volgens u 1 uitkomen...Ik dacht: +oneindig.Ook als ik deze functie teken op mijn GRM dan zie ik een verticale asymptoot bij x=1.
Hoe kan dit matchen met limieten bij logaritmen?
Dian
Leerling bovenbouw havo-vwo - vrijdag 20 december 2024

Antwoord

Je moet niet x=1 invullen, maar de limiet nemen voor x naar 1.
Je kunt 1-x\sqrt x ontbinden als (1-\sqrt x)(1+\sqrt x+x) (vermenigvuldig maar weer uit).
Het gaat dan dus om
\lim_{x\uparrow1}(1+\sqrt x+x)(1-\sqrt x)\ln(1-\sqrt x)
Van (1+\sqrt x+x) is de limiet gelijk aan 3. Dan blijft nog
\lim_{x\uparrow1}(1-\sqrt x)\ln(1-\sqrt x)
Je kunt substitueren: u=1-\sqrt x, dan staat er
\lim_{u\downarrow0} u\cdot\ln u
Dat is een bekende limiet, met waarde 0.

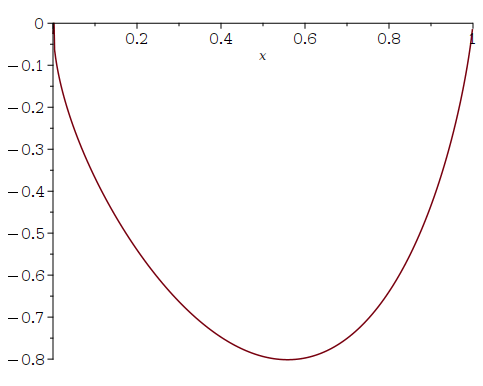Overigens, als ik de functie laat plotten krijg ik dit:Misschien deed je rekenmachine het niet helemaal goed.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 21 december 2024