WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Stelling van Thales

Hallo,

Kunnen jullie een bewijs geven van de stelling van de middenparallel, die jullie vermelden bij de stelling van Thales?

Alvast bedankt
Zie http://www.pandd.demon.nl/thales.htm
Goele
3de graad ASO - woensdag 9 april 2003

Antwoord

Stelling van de middenparallel
De lijn door het midden van een zijde van een driehoek en evenwijdig met een tweede zijde gaat door het midden van de derde zijde.

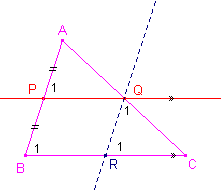
Gegeven: driehoek ABC, P is het midden van AB, Q ligt op AC, PQ // BC
Te bewijzen: AQ = QC
Bewijs:
Trek door Q een lijn QR evenwijdig met AB (met R op BC).
Nu is:
PQRB een parallellogram (paren evenwijdige zijden); dus PQ = BR
Verder
(1) QR = BP = PA (parallellogram en gegeven)
(2) R1 = B1 = P1 (F-hoeken)
(3) Q1 = A (F-hoeken)
Zodat DAPQ @ DQRC (HZH); dus AQ = QC
QED
Uit e.e.a. volgt nu ook, dat BR = RC.
N.B.
Als je op de hoogte bent van de eigenschappen van de vermenigvuldiging van figuren gaat het sneller.
De lijn PQ kan worden opgevat het beeld van een vermenigvuldiging V met centrum A (omdat PQ // BC).
Met V(B) = P zien we dat de factor gelijk is aan ¹/₂.
Dus ook V(C) = Q.
Waaruit volgt dat Q het midden is van AC.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 10 april 2003