WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Vergelijking van een cirkel

Ik moet een vergelijking opstellen van een cirkel met de oorsprong als middelpunt en bovendien moet deze cirkel de cirkel x²+y²=3x+5y-6 loodrecht snijden. Met name dit laatste gedeelte "loodrecht snijden" is mij niet duidelijk. Misschien kunnen jullie uitleggen wat daar in dit geval mee bedoeld wordt.
met vr gr
Piet
piet
Student hbo - dinsdag 8 april 2003

Antwoord

Definitie:
Twee cirkels snijden elkaar loodrecht als de raakstralen naar een snijpunt van die cirkels loodrecht op elkaar staan (zie onderstaande figuur).

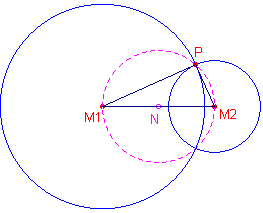
De cirkels met middelpunten M₁ en M₂ snijden elkaar loodrecht omdat ÐM₁PM₂ = 90°
In de figuur is nog een derde cirkel getekend, waarmee je bij gegeven cirkel M₂ en alleen het punt M₁ de loodrecht snijdende cirkel M₁ kan construeren:
- Bepaal het midden N van M₁M₂
- Teken de cirkel (N, NM₁)
- Noem een van de snijpunten P
- Teken de cirkel (M₁, M₁P)
Dat de hoek bij P een rechthoek is blijkt via de hulpcirkel. Waarom? Denk aan de zogenoemde Thales-cirkel.

Uit het bovenstaande blijkt dan verder dat je met behulp van de stelling van Pythagoras bij gegeven cirkel M₂ (het middelpunt en de straal zijn bekend; ze kunnen berekend worden uit de vergelijking) en gegeven coördinaten van het punt M₁, de straal van de loodrecht snijdende cirkel kan uitrekenen.
En dan is de vergelijking snel opgesteld.
Ik krijg er x² + y² = 6 uit.
Reken het nog even na (je weet maar nooit).
Als je er niet uitkomt, moet je maar even reageren.

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 8 april 2003