|
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
|||||||||||||||||
|
\require{AMSmath}



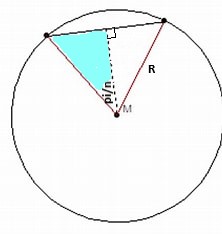
OppervlakteBewijs dat de oppervlakte S van een convexe n-hoek ingeschreven in een cirkel met straal R gegeven wordt door: S= n.R.sin(pi/n).cos(pi/n). AntwoordTwee opmerkingen. Ik denk dat het een REGELMATIGE convexe ingeschreven n-hoek moet zijn, anders geldt het namelijk niet. En zo te zien klopt je aangegeven formule ook niet.



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2025 WisFaq - versie 3 | |||||||||||||||||