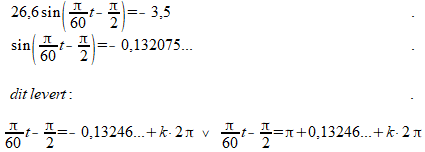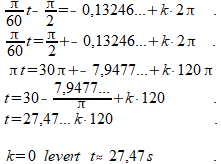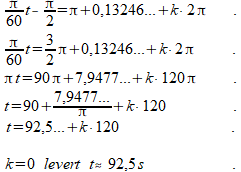|
|
|
\require{AMSmath}
Re: Re: Transformaties in de goniometrie
ik heb een soortgelijke vraag .het gaat over een reuzen rad met formule 26.5 sin ($\frac{\pi}{6}$0-$\frac{\pi}{2}$ = -3.5 $\Rightarrow$ sin($\frac{\pi}{6}$0-$\frac{\pi}{2}$ =-
0.1325.vervolgens is (pi)t/60-$\frac{\pi}{2}$=-01325 of (pi)t/60-$\frac{\pi}{2}$=01325+pi.hier ben ik verloren want waar is de sin gebleven.Daarna (pi)t/60=-01325+$\frac{\pi}{2}$=1.438 of (pi)t/60=01325+3pi snap ik niet.De uitkomst is t=1.438·60(pi)=27.46seconden of t = 92.5 sec.dit zou dan 2 keer in de eerste revolution zijn als de hoogte is 25 meters
ron
Student hbo - donderdag 9 december 2021
Antwoord
Hallo Ron,
In de opgave heb je een paar keer de variabele 't' vergeten...
Verder staat er een typfout in je uitwerking. Je noteert:
26.5 sin (pi/60-pi/2 = -3.5 =$>$ sin(pi/60-pi/2 =-0.1325
Echter, -3.5/26.5=-0,1320...
De inverse sinus van deze waarde is -0,13246. Bijna dezelfde waarde dus (dat is zo voor kleine hoeken), maar niet hetzelfde. De sinus is dus niet zomaar verdwenen.
De juiste uitwerking is als volgt:
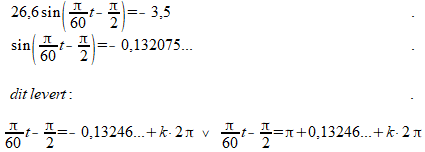
Uitwerken van de linker oplossing levert:
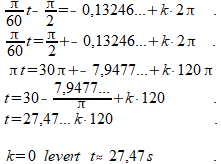
En de rechter oplossing levert:
|
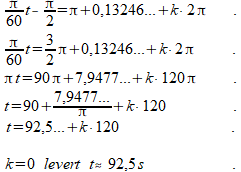
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 9 december 2021
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 93020