WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Poolcoördinaat

Goede morgen,

Gegeven: Punt P=((-sin(2),cos(2))(in radialen ).

Vraag: Als een cirkel met middelpunt (0,0) en r= 1 (x²+y²=1) vanaf (1,0) in tegenwijzerzin doorlopen wordt tot aan het punt P, dan wordt een cirkelboog beschreven waarvan de lengte L is.

Bereken L

Ik kwam daarbij L=2 uit wat ook hoort tot de mogelijke oplossingen die in het vraagstuk gegeven zijn. Maar dit is blijkbaar niet juist.

Kan wel wat hulp gebruiken.
Groetjes
Rik Le
Iets anders - donderdag 12 augustus 2021

Antwoord

Beste Rik,

Als aanvulling heb ik startpunt (1,0) en het is een meerkeuzevraag met antwoorden:

a: L$<$2
b: L=2
c: 2$<$L<$\pi$+2
d: L=$\pi$+2
e: L>$\pi$+2

Radialen zijn gedefinieerd als omtrek bij de eenheidscirkel derhalve komt ook 2$\pi$ rad overeen met 360°.

Met (-sin(2),cos(2)) kom je in het derde kwadrant (blauwe punt) uit. Dat kan je gewoon met je rekenapparaat uitrekenen. En dan weet je eigenlijk het antwoord al.

Maar ook zonder rekenmachine leg je van (-sin(0),cos(0)) ofwel punt (0,1) naar (-sin(2),cos(2)) tegen de wijzers in 2 radialen over de eenheidscirkel af en dat is meer dan 90°

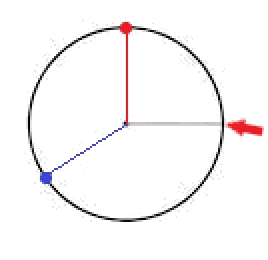
Dus van het rode punt naar het blauwe punt leg je af 2 (rad). Maar je moet starten bij de rode pijl dan komt er nog ¹/₂$\pi$ bij. Dus de afstand is exact 2+¹/₂$\pi$ radialen. En daarbij voldoet antwoord c.

Tja, ik kan me voorstellen dat die vraagstelling verwarrend over kan komen. Graag wel in het vervolg de hele vraag meenemen dus ook met alle meerkeuze antwoorden.

Met vriendelijke groet
JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 15 augustus 2021