WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

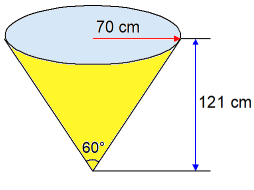
Hoogte kegel bij bekend volume en tophoek

We hebben een omgekeerde kegel met een tophoek van 60°, h=121 cm, r=70 cm. Deze willen we vullen met precies 100 liter water.
Hoe hoog is dan het niveau van het water in de deze kegel als deze met precies 100 liter gevuld is.

Sem
Leerling bovenbouw havo-vwo - zaterdag 13 juni 2020

Antwoord

Voor onze nieuwe kegel met $r$ en $h$ geldt:

$
\eqalign{
& {1 \over 3} \cdot h \cdot G = 100 \cr
& G = \pi \cdot r^2 \cr
& {r \over h} = {{70} \over {121}} \cr}
$

Met de laatste vergelijking kan je $r$ uitdrukken in $h$. Dan kan je met de tweede vergelijking $G$ uitdrukken in $h$ en dan met de eerste vergelijking $h$ berekenen.

Ik kwam uit op ongeveer 65,8 cm.

Zou dat lukken?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 13 juni 2020